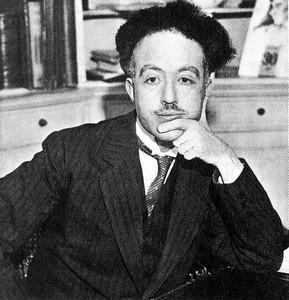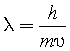Relation de de Broglie
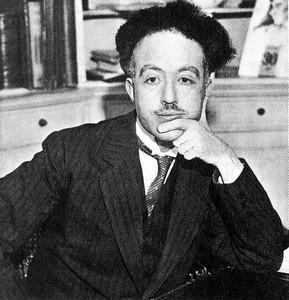
Prince Louis-Victor de Broglie (1892-1987), Prix Nobel 1929.
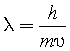
où λ est la longueur de l'onde d'une particule de masse m qui se déplace à une vitesse v.
On observe les propriétés ondulatoires d'un objet en mouvement lorsque la longueur d'onde de l'objet λ est du même ordre de grandeur¹ que les dimensions de l'espace dans lequel il est confiné.
Illustration
i.1
Calculez la longueur d'onde associée aux objets en mouvement suivants:
- Un étudiant de 75 kg, qui s'assoupit pendant le cours de Structure et tombe de sa chaise à une vitesse de 5 m/s;
- une balle de baseball (145g) qui se déplace vers le monticule à 78 miles/h (35 m/s);
- l'électron d'un atome d'hydrogène dans le modèle de Bohr, dans son état fondamental;
- pour lesquels de ces objets pourra-t-on observer des propriétés ondulatoires?
a)1.8×10-36 m; b) 1.3×10-34 m; c) 3.3Å; d) l'électron.
i.2
Une balle de ping-pong, de masse 2.7 g et de diamètre 40 mm, se déplace à une vitesse de 9 km/h.
- Calculez la longueur d'onde associée aux propriétés ondulatoires de la balle;
- On peut imaginer qu'il existe peut-être d'autres univers où les constantes fondamentales ont des valeurs différentes que dans le notre. Quelle devrait être environ la valeur de la constante de Planck pour qu'il soit possible d'observer les propriétés ondulatoires de la balle de ping-pong ?
a)λ = 9.816×10-32 m; b) 10-3 à 10-4 J.s
¹L'ordre de grandeur est une fourchette de valeurs qui va d'un dixième à dix fois la grandeur environ. Ainsi, on dira qu'un nombre X est du même ordre de grandeur qu'un nombre Y lorsque Y/10 ≤ X ≤ 10Y environ.