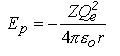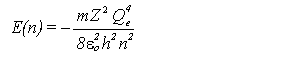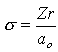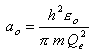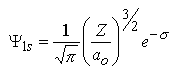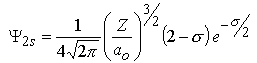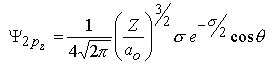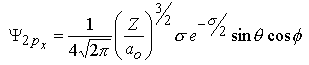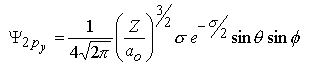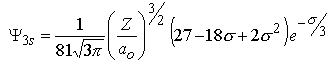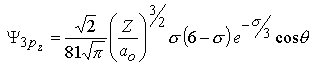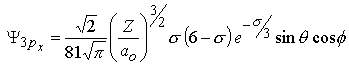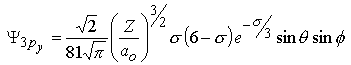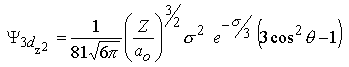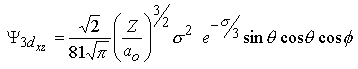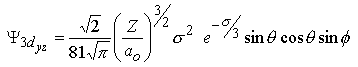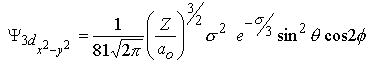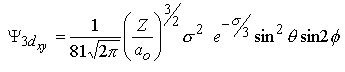Atome d'hydrogène et autres espèces atomiques monoélectroniques
Dans l'atome d'hydrogène et dans les ions contenant un seul électron, comme He+, Li2*, etc., l'électron se trouve dans le champ d'un noyau contenant Z protons. Son énergie potentielle est une fonction de la distance au noyau, r:
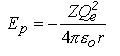
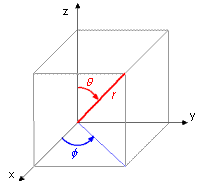
La résolution de l'équation de Schrödinger requiert d'exprimer la position de tout point de l'espace par ses coordonnées polaires r, θ et Φ, comme le montre la figure ci-contre.
Solutions de l'équation de Schrödinger
L'énergie de l'électron est:
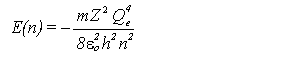
où n est un entier strictement positif. Cette expression est identique au résultat de Bohr, ce qui explique le succès de ce dernier modèle pour reproduire le spectre de raies des espèces monoélectroniques.
Les fonctions d'onde obtenues, qu'on appelle orbitales, sont définies par 3 nombres quantiques:
- le nombre quantique principal, n, déja rencontré dans l'expression de l'énergie, et qui peut prendre toute valeur entière strictement positive;
- le nombre quantique de moment angulaire, l, qui peut prendre n valeurs entières de 0 à (n-1);
-
le nombre quantique magnétique, m, qui peut avoir (2l+1) valeurs de -l à +l (y compris zéro).
L'usage est de désigner les orbitales par la valeur de n et une lettre, choisie selon la valeur de l:
|
|
| s | p | d | f | g |
|
|
pour l = | 0 | 1 | 2 | 3 | 4 |
Afin de simplifier les équations des fonctions d'onde, on utilise σ pour exprimer la distance électron-noyau:
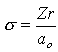
où ao est le rayon de la première orbite de Bohr:
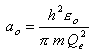
| n=1 |
l=0 |
m=0 |
|
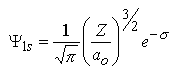
| n=2 |
l=0 |
m=0 |
|
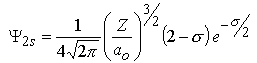
| l=1 |
m=0 |
 |
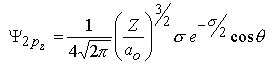| m=±1 |
 |
 |
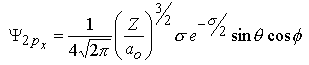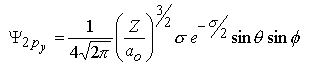| n=3 |
l=0 | m=0 |
|
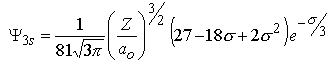
| l=1 |
m=0 |
 |
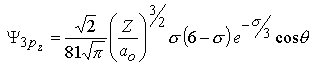| m=±1 |
 |
 |
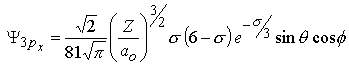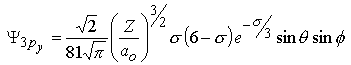| l=2 |
m=0 |
 |
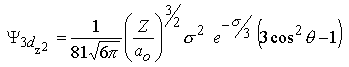| m=±1 |
 |
 |
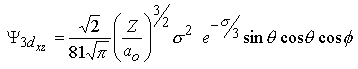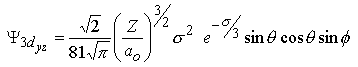| m=±2 |
 |
 |
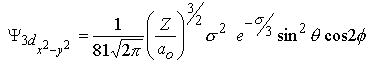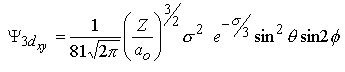Représentation des orbitales
Densité de probabilité
La probabilité de présence de l'électron dans un volume dV situé en un point de l'espace est Ψ2dV. Le terme Ψ2 est appelé la densité de probabilité.
La probabilité de présence de l'électron dans un volume dV situé à une distance r du noyau, quelle que soit la direction, est 4πr2Ψ2dV. Le terme 4πr2Ψ2 est la densité de probabilité radiale:
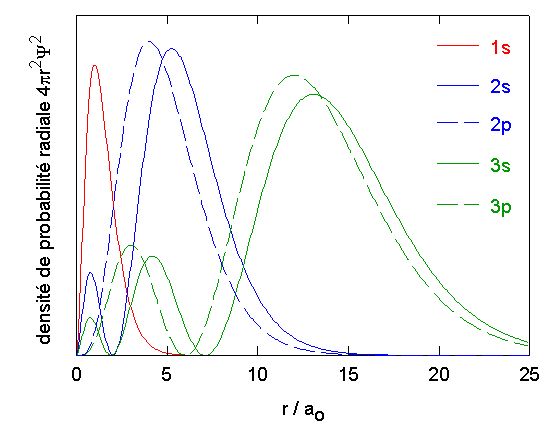
Remarques:
-
L'échelle de l'ordonnée est différente pour chaque fonction, afin de faciliter la comparaison.
-
La densité de probabilité pour 1s est maximum pour r = ao.
-
Notez l'origine de la notion de couche, la densité de probabilité étant la plus grande dans un domaine de r qui ne dépend approximativement que de n:
- couche K pour r autour de ao (orbitale 1s)
- couche L pour r autour de 4 à 6 fois ao (orbitales 2s, 2p)
- couche M pour rautour de 10 à 16 fois ao (orbitales 3s, 3p)
- Notez également que, même si l'essentiel de la probabilité de présence de l'electron 2s se trouve autour de 5ao, il peut également se trouver, avec une probabilité non négligeable, plus près du noyau, à une distance similaire à celle de l'électron 1s. C'est aussi le cas de 3s, par exemple.
Autres représentations
Les trois images sont des représentations de la même orbitale, ici 3dz2
Représentations interactives (requiert Java)
