| 3.1 |
Calculer la quantité de mouvement d'un photon de longueur d'onde égale à 500 nm.
|
|
Réponse: 1.325×10 -27 kg.m.s-1
|
| 3.2 |
En diffraction électronique, on peut ajuster la longueur d'onde des électrons en changeant leur vitesse. Quelle vitesse doit-on leur donner pour que leur longueur d'onde soit 1nm?
|
|
Réponse:
727 km.s -1
|
| 3.3 |
On considère un électron confiné sur une boite unidimensionnelle de longueur L=2Å.
- Calculer les deux plus basses énergies permises.
- calculer la longueur d'onde de la radiation permettant d'exciter l'électron de son niveau fondamental au premier niveau excité.
- Calculer la probabilité que l'électron dans l'état fondamental se trouve à ±0.5Å du centre de la boite.
- Que devient cette probabilité lorsque l'électron se trouve dans le premier niveau excité.
|
Réponse:
a) 1.506×10 -18 et 6.025×10 -18 J; b) 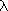 = 43.96 nm; c) 0.818; d) 0.500 = 43.96 nm; c) 0.818; d) 0.500
|
| 3.4 |
Un électron est confiné dans une boite unidimensionnelle de longueur L = 10 Å.
- Calculer les quatre plus grandes longueurs d'onde du spectre de raies de ce système. Représenter schématiquement sur un diagramme d'énergie les transitions correspondant à ces raies.
- Tracer (à l'aide d'un logiciel ou sur un papier millimétré) la densité de probabilité de l'électron en fonction de sa position dans la boite, dans l'état fondamental et dans le premier état excité.
- Calculer la probabilité de présence de l'électron à ±1Å du centre de la boite, dans l'état fondamental et dans le premier état excité.
- Les résultats numériques obtenus dans la question c) sont-ils en accord avec les tracés de la question b).
|

|
| 3.5 |
Le butadiène CH2=CH-CH=CH2 est une molécule possédant 4 électrons 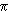 délocalisés. Montrer qu'un modèle de la molécule où ces électrons se comportent comme des particules dans une boite de longueur 5.8 Å permet d'expliquer que la longueur d'onde la plus grande du spectre d'absorption du butadiène dans l'UV se trouve à 217 nm (il faut noter que chaque fonction d'onde ne peut décrire les propriétés de plus de 2 électrons). délocalisés. Montrer qu'un modèle de la molécule où ces électrons se comportent comme des particules dans une boite de longueur 5.8 Å permet d'expliquer que la longueur d'onde la plus grande du spectre d'absorption du butadiène dans l'UV se trouve à 217 nm (il faut noter que chaque fonction d'onde ne peut décrire les propriétés de plus de 2 électrons).
|

|
| 3.6 |
La résolution de l'équation de Schrödinger pour une particule confinée dans une boite bidimensionnelle carrée de coté a conduit à:
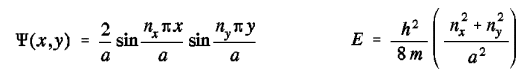
où 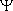 (x,y) est la fonction d'onde de la particule, E son énergie et nx et ny sont deux nombres quantiques pouvant prendre indépendamment n'importe quelle valeur entière strictement positive. (x,y) est la fonction d'onde de la particule, E son énergie et nx et ny sont deux nombres quantiques pouvant prendre indépendamment n'importe quelle valeur entière strictement positive.
Ce modèle de particule confinée sur une surface décrit approximativement les électrons des porphyrines métalliques, telles l'hémoglobine ou la chlorophylle. Ainsi, une porphyrine typique contient 26 électrons confinés sur un carré de 1 nm de coté.
- Représenter schématiquement tous les niveaux d'énergie permis entre 0 et
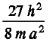
- Placer les 26 électrons sur ces niveaux, sachant que chaque fonction d'onde ne peut décrire les propriétés de plus de 2 électrons.
- La longueur d'onde la plus grande mesurée sur le spectre d'absorption de cette molécule est
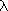 max=600 nm. Calculer la valeur de max=600 nm. Calculer la valeur de 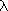 max prédite par le modèle. max prédite par le modèle.
|
Réponse:
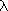 max = 659 nm max = 659 nm
|
| 3.7 |
Les orbitales de l'atome d'hydrogène sont décrites par trois nombres quantiques: n, 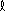 et m. et m.
- Si n = 2 et m = -1, quelles sont toutes les valeurs possibles de
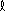 ? ?
- Si n = 2 et m = 0, quelles sont toutes les valeurs possibles de
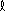 ? ?
- Si
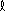 = 2 et n = 3, quelles sont toutes les valeurs possibles de m ? = 2 et n = 3, quelles sont toutes les valeurs possibles de m ?
- Si
 = 0 et n = 5, quelles sont toutes les valeurs possibles de m ? = 0 et n = 5, quelles sont toutes les valeurs possibles de m ?
- Si m = 1 et
 = 1, quelles sont toutes les valeurs possibles de n ? = 1, quelles sont toutes les valeurs possibles de n ?
|
| 3.8 |
Parmi les ensembles de nombres quantiques suivants, indiquer, en expliquant pourquoi, lesquels ne sont pas permis pour l'atome d'hydrogène:
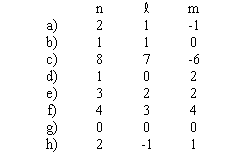
|

