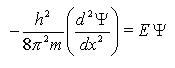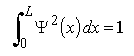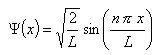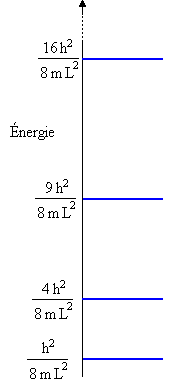Particule confinée dans une boite unidimensionnelle
Pour une particule qui se déplace librement sur un segment de droite, de longueur L et tel que l'énergie potentielle Ep est nulle sur le segment et infiniment grande partout ailleurs (particule dans une boite), l'équation de Schröedinger se simplifie en:
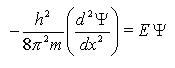
La résolution de cette équation différentielle conduit à une infinité de solutions. Cependant, les seules solutions acceptables sont celles qui vérifient:
- les valeurs aux bornes:
La particule se trouve sur le segment et non à l'extérieur, où Ep est +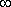
. La fonction d'onde, dont le carré mesure la densité de probabilité de présence de la particule, est par conséquent nulle à l'extérieur de la boite. Puis que 
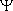est une fonction continue, on doit avoir
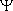(0)=0 et 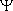(L)=0
- la condition de normalisation:
La probabilité de présence de la particule sur le segment entier, c'est-à-dire x entre 0 et L, est 100%:
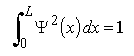
On obtient finalement, pour les fonctions d'ondes:
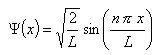
et pour l'énergie:
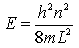
où le nombre quantique n est un entier strictement positif.
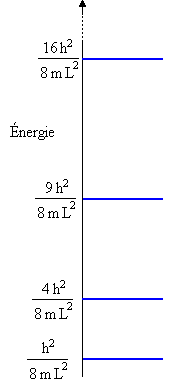
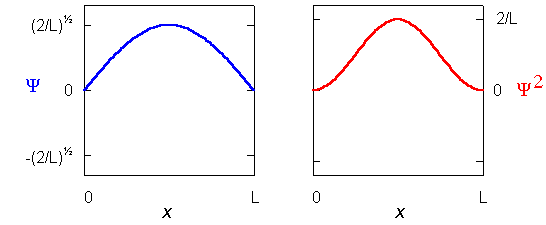
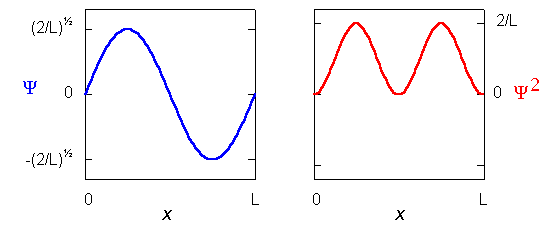
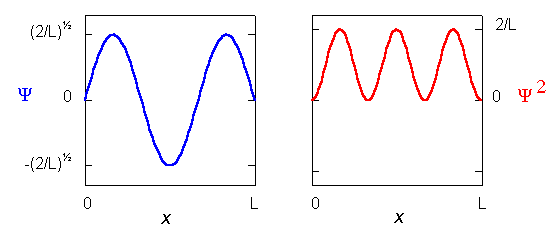
La variation de la fonction d'onde 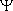et de la densité de probabilité 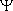2 en fonction de la position dans la boite dépend de n:
Que se passe-t-il si on place plus d'un électron dans une boite unidimensionnelle?
Les solutions de l'équation de Schrödinger sont les même (mêmes fonctions d'onde, mêmes énergies) mais il y a au plus deux électrons dont les propriétés ondulatoires sont décrites par une fonction d'onde donnée (principe d'exclusion de Pauli). On aura donc ici, à l'état fondamental) au plus deux électrons de fonction d'onde n=1. Un troisième électron dans la boite aurait (même à l'état fondamental) la fonction d'onde et l'énergie correspondant à n=2.
Exercice d'application
Les polyènes conjugués linéaires sont des molécules constituées de liaisons carbone-carbone doubles et simples en alternance. Le butadiène, H2C=CH-CH=CH2, l’hexatriène, H2C=CH-CH=CH-CH=CH2, et l’octatétraène, H2C=CH-CH=CH-CH=CH-CH=CH2, en sont des exemples Ces molécules possèdent des électrons délocalisés, 2 pour chaque liaison C=C, dont les propriétés ondulatoires obéissent au modèle de particules dans une boite à une dimension. Sachant que chaque liaison carbone-carbone simple ou double contribue en moyenne 1.390Å à la longueur de la boite :
- Calculer, pour chacune des trois molécules données en exemple, la longueur d’onde maximum du spectre d’absorption;
- déterminer le nombre de doubles liaisons dans le polyène de cette série qui possède un maximum d’absorption à une longueur d’onde égale à 843 nm.
