

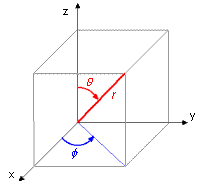
 Dans l'atome d'hydrogène et dans les ions contenant un seul électron, comme He+, Li2*, etc., l'électron se trouve dans le champ d'un noyau contenant Z protons. Son énergie potentielle est une fonction de la distance au noyau, r:
Dans l'atome d'hydrogène et dans les ions contenant un seul électron, comme He+, Li2*, etc., l'électron se trouve dans le champ d'un noyau contenant Z protons. Son énergie potentielle est une fonction de la distance au noyau, r:

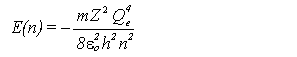
| s | p | d | f | g | ||
| pour | 0 | 1 | 2 | 3 | 4 |
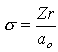
|
où ao est le rayon de la première orbite de Bohr: |
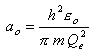
|
| n=1 |
|
m=0 | 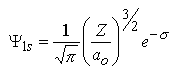 |  |
| n=2 | |
m=0 | 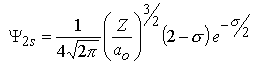 |  |
| |
m=0 | 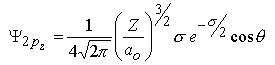 |  |
|
| m=±1 | 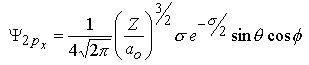 | |||
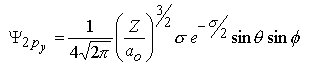 |
||||
| n=3 | | m=0 | 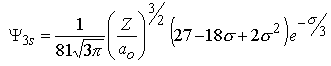 | |
| |
m=0 | 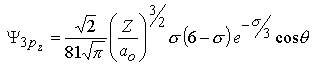 |  |
|
| m=±1 | 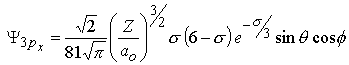 | |||
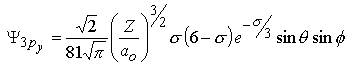 | ||||
| |
m=0 | 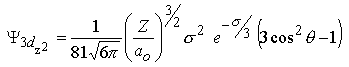 |  | |
| m=±1 | 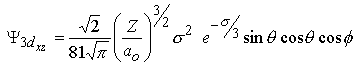 |  |
||
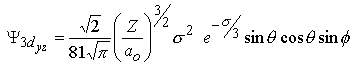 | ||||
| m=±2 | 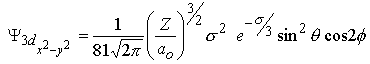 |  |
||
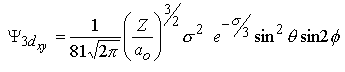 |
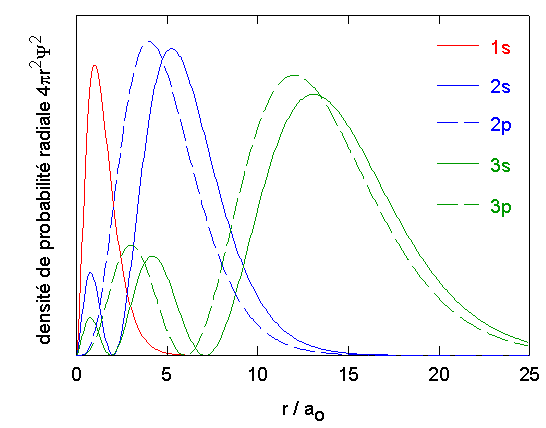
| 1s | 2s | |

|

|
|
| 2pz | 3pz | |

|

|

|
| 3pz | 3dyz | 3dz2 | |

|

|
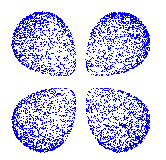
|

|