Énoncé
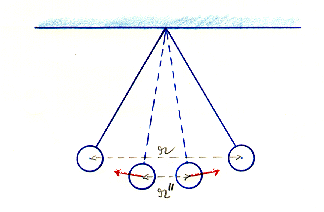
On attache deux balles de ping-pong à un même point du plafond, chacune au bout d'un fil mince d'une longueur égale à 60 cm. Chaque balle pèse 10 g. On confère à chacune de deux balles une charge identique et on observe alors que les balles se repoussent à une distance de 60 cm. Quelle est la charge de chaque balle?
Représenter schématiquement la variation de l'énergie potentielle des deux balles en fonction de la distance qui les sépare.
Réponse
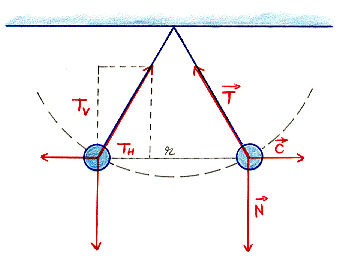
Les balles possède chacune une charge identique, Q. Par conséquent, elles se repoussent avec une force de Coulomb 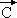 dont le module est:
dont le module est:
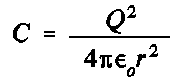
où r est la distance qui sépare les deux balles.
Les balles possèdent chacune une masse m et sont donc soumises à une force de Newton 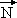 , dirigée vers le bas, de module:
, dirigée vers le bas, de module:
N = m g
où g est le module du champ gravitationnel.
À l`équilibre, les balles sont immobiles lorsque la résultante de
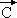 ,
,
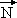 et
de la force de tension du fil,
et
de la force de tension du fil, 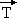 , est nulle. C'est le cas lorsque:
, est nulle. C'est le cas lorsque:
- le module de la composante de
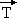 sur l'axe horizontal, TH est égal à C
sur l'axe horizontal, TH est égal à C
- le module de la composante de
 sur l'axe vertical, TV est égal à N
sur l'axe vertical, TV est égal à N
Si on note ß l'angle entre les deux fils de longueur l, qui relient les balles au plafond, on a:
On nous dit que la distance entre les balles à l'équilibre est r = 60 cm, identique à l. Le triangle est donc équilatéral et l'angle ß est 60°. Donc,
ce qui conduit à Q = 1.506×10-6 C ou 1.506 µC.
Variation de l'énergie potentielle des balles en fonction de r
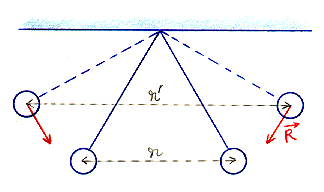 Pour augmenter la distance entre les 2 balles de r à r', l'observateur doit fournir de l`énergie sous forme de travail car la résultante des forces
Pour augmenter la distance entre les 2 balles de r à r', l'observateur doit fournir de l`énergie sous forme de travail car la résultante des forces 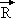 =
=
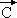 +
+
 +
+
 s'oppose au déplacement. Ce travail dépensé par l'observateur est gagné par les balles qui voient donc leur énergie potentielle EP augmenter.
s'oppose au déplacement. Ce travail dépensé par l'observateur est gagné par les balles qui voient donc leur énergie potentielle EP augmenter.
 C'est la même chose si l'observateur diminue la distance de r à r''.
C'est la même chose si l'observateur diminue la distance de r à r''.
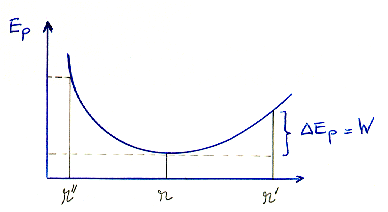 Bien que l'on ne connaisse pas la valeur absolue de EP, on peut tracer l'allure de EP en fonction de r. Celle-ci augmente pour toute valeur de r plus grande ou plus petite que la valeur d'équilibre. Cette augmentation est d'autant plus grande que le déplacement est grand. L'énergie potentielle est minimum pour r égal à la valeur d'équilibre.
Bien que l'on ne connaisse pas la valeur absolue de EP, on peut tracer l'allure de EP en fonction de r. Celle-ci augmente pour toute valeur de r plus grande ou plus petite que la valeur d'équilibre. Cette augmentation est d'autant plus grande que le déplacement est grand. L'énergie potentielle est minimum pour r égal à la valeur d'équilibre.




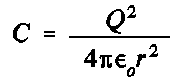
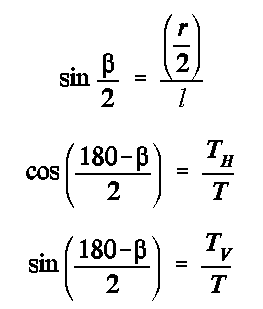
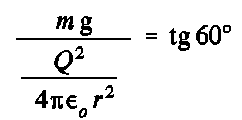
 Pour augmenter la distance entre les 2 balles de r à r', l'observateur doit fournir de l`énergie sous forme de travail car la résultante des forces
Pour augmenter la distance entre les 2 balles de r à r', l'observateur doit fournir de l`énergie sous forme de travail car la résultante des forces ![]() =
=
![]() +
+
![]() +
+
![]() s'oppose au déplacement. Ce travail dépensé par l'observateur est gagné par les balles qui voient donc leur énergie potentielle EP augmenter.
s'oppose au déplacement. Ce travail dépensé par l'observateur est gagné par les balles qui voient donc leur énergie potentielle EP augmenter.
 C'est la même chose si l'observateur diminue la distance de r à r''.
C'est la même chose si l'observateur diminue la distance de r à r''.
 Bien que l'on ne connaisse pas la valeur absolue de EP, on peut tracer l'allure de EP en fonction de r. Celle-ci augmente pour toute valeur de r plus grande ou plus petite que la valeur d'équilibre. Cette augmentation est d'autant plus grande que le déplacement est grand. L'énergie potentielle est minimum pour r égal à la valeur d'équilibre.
Bien que l'on ne connaisse pas la valeur absolue de EP, on peut tracer l'allure de EP en fonction de r. Celle-ci augmente pour toute valeur de r plus grande ou plus petite que la valeur d'équilibre. Cette augmentation est d'autant plus grande que le déplacement est grand. L'énergie potentielle est minimum pour r égal à la valeur d'équilibre.