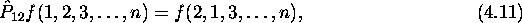
On peut aisément vérifier que l'hamiltonien de (4.1) est invariant dans la permutation, c.à.d. dans l'échange de deux indices électroniques données, 1 et 2 par exemple. En introduisant l'opérateur de permutation
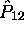 défini par
défini par
on peut exprimer cette propriété de symétrie de l'hamiltonien par
ou encore, puisque 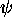 dans cette équation est arbitraire,
dans cette équation est arbitraire,
Ceci signifie que les fonctions propres de 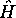 peuvent être
construites fonctions propres de
peuvent être
construites fonctions propres de 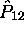 aussi. En d'autres termes,
elles sont d'un caractère bien déterminé par rapport à cette
opération de symétrie, la permutation
aussi. En d'autres termes,
elles sont d'un caractère bien déterminé par rapport à cette
opération de symétrie, la permutation 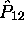 . Cette conclusion
tient pour toute permutation
. Cette conclusion
tient pour toute permutation 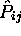 de paire
de paire 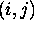 d'indices
électroniques. En fait, elle est vraie pour n'importe quel
système de particules identiques, indiscernables, dont
l'indiscernabilité se traduit précisément par l'invariance de
l'hamiltonien dans ce genre d'opération de symétrie. On constate
maintenant que
d'indices
électroniques. En fait, elle est vraie pour n'importe quel
système de particules identiques, indiscernables, dont
l'indiscernabilité se traduit précisément par l'invariance de
l'hamiltonien dans ce genre d'opération de symétrie. On constate
maintenant que
ce qui implique que 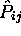 ne peut avoir que deux valeurs propres,
soit +1 et -1. Par conséquent les fonctions d'onde décrivant les
états stationaires d'un système de particules identiques ne
peuvent être que symétriques (paires) ou antisymétriques
(impaires) par rapport aux permutations
ne peut avoir que deux valeurs propres,
soit +1 et -1. Par conséquent les fonctions d'onde décrivant les
états stationaires d'un système de particules identiques ne
peuvent être que symétriques (paires) ou antisymétriques
(impaires) par rapport aux permutations 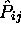 . Lequel de ces deux
caractères de symétrie s'applique à un système donné dépend de
la nature des particules identiques constituant ce système, et
est dicté par le principe de Pauli.
. Lequel de ces deux
caractères de symétrie s'applique à un système donné dépend de
la nature des particules identiques constituant ce système, et
est dicté par le principe de Pauli.