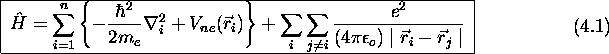
L'opérateur hamiltonien d'un système atomique ou moléculaire à n électrons est
où
dans le cas d'un atome, et
dans le cas d'un système moléculaire à N noyaux.
On note, à l'examen de (4.1), que sans le dernier terme, qui représente l'interaction coulombienne entre les électrons, l'hamiltonien serait de forme séparable. L'existence de cette interaction entre les électrons rend la résolution de l'équation de Schrödinger considérablement plus difficile.
Dans une approximation dite approximation des électrons
indépendants, on part de l'idée que chaque électron sent la
présence des autres électrons à travers un potentiel effectif
moyen qui tend à réduire les forces d'attraction nucléaire; on
dit alors que le potentiel d'attraction nucléaire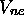 
est
écranté. On écrit alors l'hamiltonien exact de
(4.1) sous la forme
où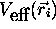 
est le potentiel effectif
mentionné ci-haut.
C'est un potentiel mono-électronique, étant donné que le potentiel
de répulsion coulombienne inter-électronique a déjà été
moyenné sur la distribution des n-1 électrons autres que
l'électron en considération (le i-ème). La construction de
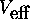dépend du niveau d'approximation auquel on effectue cette
moyenne dans le traitement du système multi-électronique. Plus le terme résidual 
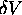est faible, plus l'approximation des électrons indépendants considéré est bonne. Il n'existe
donc pas une approximation ou un modèle des électrons
indépendants unique. Le procédé qu'on vient d'esquisser définit
plutôt une classe de modèles des électrons indépendants.
