Une conséquence de la forme déterminantale de la fonction d'onde, (4.28), est le principe d'exclusion: Si deux colonnes du déterminant de (4.27), c'est-à-dire si deux spin- orbitales, sont identiques, alors la fonction d'onde est nulle partout. On obtient alors la solution triviale de l'équation de Schrödinger qui dénote une situation non physique, que l'on doit écarter. Par conséquent, on peut énoncer que:
Principe d'exclusion
Il est important de souligner que ce principe d'exclusion est un corollaire du principe de Pauli, et il n'est applicable que dans le cadre d'un modèle des électrons indépendants. En effet, la forme déterminantale de la fonction d'onde n'est obtenue que dans un tel cadre, et est une conséquence du fait que les électrons sont des fermions.
Répulsion de Pauli: Il existe une forme plus générale du principe d'exclusion. Elle découle directement du caractère antisymétrique de la fonction d'onde d'un système de N électrons,
qui implique que la fonction d'onde est nulle dans le cas où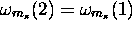 
et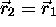 
. On peut donc énoncer
Deux électrons (fermions) de même spin ne peuvent jamais se trouver au même endroit.
Cet énoncé est tout à fait général; il ne dépend pas de l'approximation des électrons indépendants. Il implique que, même si les deux électrons étaient indépendants l'un de l'autre, ils tendent à s'éviter, et leur mouvement apparait 'corrélé'. Cette répulsion de deux fermions indépendants de même spin est strictement un effet du principe de Pauli; on peut l'appeler, pour cette raison, répulsion de Pauli. Elle s'opère sans qu'aucune force n'est mise à contribution, sans qu'aucun travail soit effectué. Dans le cas d'un système à plusieurs électrons, fermions chargés interagissant à travers des forces de Coulomb, la répulsion de Pauli tente à favoriser des configurations avec un nombre maximal de spins parallèles, car l'éloignement de ces spins abaisse l'énergie de répulsion coulombienne et stabilise le système. Cette tendance est résumée par une des règles appellée règles de Hund.
