Les électrons étant des fermions (
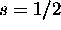), le principe de Pauli
demande que la fonction d'onde électronique soit symétrique par
rapport aux permutations 
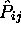. D'autre part, on a vu que dans un
modèle des électrons indépendants, la fonction d'onde électronique
serait un produit du type représenté en (4.7). Une
telle forme produit n'est malheureusement pas antisymétrique. Par
exemple, si l'on considère l'atome d'Hélium traité dans le modèle
des électrons indépendants le plus simple, celui obtenu en posant
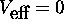, alors son état fondamental correspondra à un
produit du type
où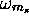 
est une fonction de spin et 
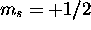ou
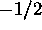. On a donc quatre fonctions pouvant décrire l'état
fondamnental du système, avant l'imposition du principe de Pauli:
On vérifie aisément que
c'est-à-dire que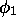 
et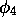 
sont symétriques par
rapport à la permutation des deux électrons, tandis que
c'est-à-dire que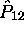 
échange les deux fonctions 
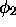et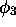 
. Elles ne sont pas fonctions propres de cet opérateur de
permutation. Aucune des quatre fonctions ne se conforme donc au principe
de Pauli. On note cependant que ces fonctions correspondent à la
même valeur d'énergie
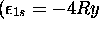, car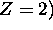 
, et toute combinaison linéaire
de ces quatre fonctions serait aussi fonction propre de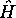 
avec
la même valeur propre, dans la même approximation. Parmi toutes les
combinaisons linéaires possibles des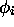 
, une seule satisfait
au principe de Pauli; elle se lit
C étant une constante de normalisation qui vaut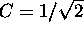 
.
La fonction antisymétrique que l'on vient de définir,
(4.24), peut se mettre sous la forme d'un déterminant
appelé déterminant de Slater. On note que la fonction n'est plus
un simple produit; cependant, due à l'orthogonalité des spin-
orbitales qui y figurent, la densité de probabilité de présence
des deux électrons continue à être décrite par un simple
produit des densités individuelles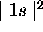 
Ceci n'est malheureusement vrai que dans ce cas particulier où les deux électrons ont leur spin opposés. Dans le cas de deux spins parallèles, la densité de probabilité de présence des deux électrons doit nécessairement être différente de celle de deux électrons indépendants, (voir la section suivante sur le principe d'exclusion, et le problème 4 de la série d'exercices, section 4.5). La construction précédente se généralise à n'importe quel état stationaire d'un système multiélectronique quelconque, traité dans l'approximation des électrons indépendants: En partant d'un produit de la forme de (4.7)
où les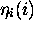 
sont des spin-orbitales du système
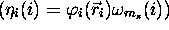, on
obtient une fonction d'onde antisymétrique
normée en construisant le déterminant de Slater suivant
Chaque colonne de ce déterminant correspond à une spin-orbitale, chaque rangée à un électron (une indice
électronique). Le produit des termes figurant sur la diagonale
principale du déterminant est précisément le produit de départ,
(4.27). Par le même raisonnement que celui utilisé
ci-haut pour l'état fondamental de He, l'état représenté par ce
déterminant est de même énergie que l'état décrit par
(4.27). Le principe de Pauli dicte l'emploi de la
fonction d'onde antisymétrique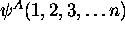 
, à la
place du produit de (4.27).
