-
Le modèle des électrons indépendants le plus simple pour He
est obtenu en négligeant complètement l'interaction coulombique
entre les deux électrons du système. Écrivez l'hamiltonien
effectif monoélectronique
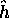 de ce modèle et donnez la forme
générale a) des orbitales, b) des spin-orbitales et c) des
énergies orbitalaires de ce système. Calculez le premier et le
second potentiel d'ionisation de l'atome dans cette
approximation. Comparez vos résultats avec les valeurs
expérimentales suivantes:
de ce modèle et donnez la forme
générale a) des orbitales, b) des spin-orbitales et c) des
énergies orbitalaires de ce système. Calculez le premier et le
second potentiel d'ionisation de l'atome dans cette
approximation. Comparez vos résultats avec les valeurs
expérimentales suivantes:
- premier potentiel d'ionisation
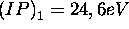
- second potentiel d'ionisation
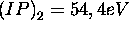
À la lumière de vos observations, critiquez ce modèle.
- premier potentiel d'ionisation
- Dans un traitement très grossier d'un système linéaire de
liaisons
 conjuguées, on considère que les électrons
conjuguées, on considère que les électrons 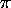 se
meuvent dans un potentiel uni-dimensionnel moyen tel que
se
meuvent dans un potentiel uni-dimensionnel moyen tel que 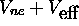 est constant (nul) si la position x de l'électron le
long de la chaîne de liaisons
est constant (nul) si la position x de l'électron le
long de la chaîne de liaisons 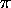 (dont la longueur est L) satisfait
0 < x < L, et infini ailleurs. On appelera ce modèle 'modèle particules
dans une boîte''.
(dont la longueur est L) satisfait
0 < x < L, et infini ailleurs. On appelera ce modèle 'modèle particules
dans une boîte''.
Déterminez a) les orbitales, b) les énergies orbitalaires et c) les spin-orbitales d'un tel système.
- Pour étudier très qualitativement le comportement des six
électrons
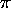 dans le benzène, on propose que ces électrons
puissent être considérés comme des particules indépendantes se
mouvant sur un cercle de rayon
dans le benzène, on propose que ces électrons
puissent être considérés comme des particules indépendantes se
mouvant sur un cercle de rayon 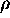 fixé, situé sur le plan xz.
L'hamiltonien de ce système est
fixé, situé sur le plan xz.
L'hamiltonien de ce système est

avec
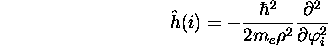
où
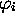 est l'angle formé par le vecteur de position du i-ème
électron (dans le plan) et l'axe z. Montrez que
est l'angle formé par le vecteur de position du i-ème
électron (dans le plan) et l'axe z. Montrez que
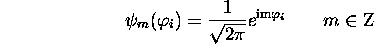
sont des orbitales dans ce modèle, dit 'particules sur un cercle', du benzène. Dressez un diagramme montrant les trois premiers niveaux d'énergie orbitalaire de ce système, avec leur dégénérescence respective.
- Considérons deux électrons 'de même spin', c'est à dire décrits par la même fonction de spin,
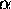 , disons.
, disons.
- En vous plaçant dans l'approximation des électrons indépendants,
montrez que les deux électrons doivent nécessairement être décrits par
des orbitales
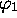
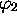 différentes.
différentes.
- Montrez que le déterminant de Slater décrivant l'état du système formé de ces deux électrons dans les spinorbitales précitées se factorise en
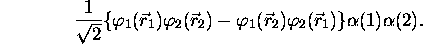
- Vérifiez que ces deux électrons de même spin ne peuvent pas se trouver au même endroit, c.à d. que l'on ne peut pas avoir

- En vous plaçant dans l'approximation des électrons indépendants,
montrez que les deux électrons doivent nécessairement être décrits par
des orbitales
- En respectant le principe de Pauli, construisez la fonction
d'onde de l'état fondamental de l'éthylène (un système de 2
électrons
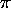 ) dans le modèle `particules dans une boîte'
considéré ci-haut pour les systèmes de liaisons
) dans le modèle `particules dans une boîte'
considéré ci-haut pour les systèmes de liaisons 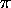 conjuguées.
conjuguées.
- Écrivez la configuration de l'état fondamental du butadiène,
un système de 4 électrons
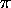 (2 liaisons
(2 liaisons 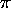 conjuguées),
dans le même modèle. Quelle en serait l'énergie totale?
conjuguées),
dans le même modèle. Quelle en serait l'énergie totale?
- En respectant le principe de Pauli, écrivez a) la configuration électronique, b) l'énergie totale et c) la fonction d'onde totale, de l'état fondamental du benzène décrit dans le modèle `particules sur un cercle'.
- On donne au tableau 5.3 les premier et deuxième potentiels d'ionisation ainsi que l'affinité électronique des huit éléments de la seconde période du tableau périodique. On rappelle que l'affinité électronique,
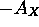 d'un élément X est aussi le premier potentiel d'ionisation de l'anion
d'un élément X est aussi le premier potentiel d'ionisation de l'anion 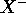 :
:
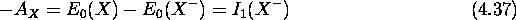
- En supposant que l'électron périphérique de
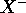 est dans une orbitale hydrogénoïde, calculez la charge nucléaire effective,
est dans une orbitale hydrogénoïde, calculez la charge nucléaire effective, 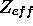 , ressentie par cet électron dans
, ressentie par cet électron dans 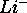 ,
, 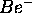 ,
, 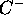 ,
, 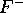 , a) directement de la valeur de
, a) directement de la valeur de 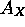 , b) en employant les règles de Slater.
, b) en employant les règles de Slater.
- En supposant que l'électron périphérique de
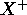 est dans une orbitale hydrogénoïde, calculez la charge nucléaire effective,
est dans une orbitale hydrogénoïde, calculez la charge nucléaire effective, 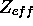 , ressentie par l'électron périphérique de
, ressentie par l'électron périphérique de 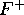 . À partir de ce résultat, et des résultats de la question précédente, et en employant la relation
. À partir de ce résultat, et des résultats de la question précédente, et en employant la relation
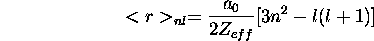
qui donne, exactement, la valeur moyenne du rayon r d'un atome hydrogénoïde, de charge nucléaire
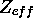 , dans l'état
, dans l'état 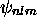 ,
estimez le rayon moyen, (en unité atomique, le Bohr,
,
estimez le rayon moyen, (en unité atomique, le Bohr, 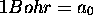 ), de
), de 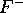 et de
et de 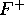 . Comment peut-on expliquer la différence de taille de ces deux ions?
. Comment peut-on expliquer la différence de taille de ces deux ions?
- Il est intéressant de comparer les variations de
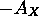 sur la deuxième période, à celles de
sur la deuxième période, à celles de 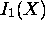 . En vous reférant à la structure électronique de l'anion
. En vous reférant à la structure électronique de l'anion 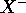 , donnez une explication rationnelle aux observations suivantes:
, donnez une explication rationnelle aux observations suivantes:
-
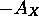 atteint un maximum pour
atteint un maximum pour 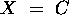 tandis que
tandis que 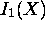 atteint un maximum pour
atteint un maximum pour 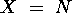 .
.
-
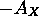 chute dramatiquement quand l'on passe de F à Ne.
chute dramatiquement quand l'on passe de F à Ne.
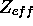 , ressentie par l'électron périphérique de l'anion et calculée par les règles de Slater?
, ressentie par l'électron périphérique de l'anion et calculée par les règles de Slater?
-
- En supposant que l'électron périphérique de
- Imaginons un monde dans lequel l'électron a un spin
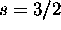 .
.
- Enumérez les valeurs possibles de
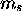 . Décrivez les états de spin électronique correspondant à chacune de ces valeurs.
. Décrivez les états de spin électronique correspondant à chacune de ces valeurs.
- Quelle serait la configuration électronique de C, Ne, Sc, Fe, S, dans ce monde? (On supposerait que les OA continuent à suivre la règle de Klechkowski)
- Esquissez la forme qu'emprunterait le tableau périodique dans ce monde:
- Combien de familles (groupes) comprendra
- le bloc s?
- le bloc p?
- Quelle type de configurations définira des éléments 'nobles' ?
- De combien de faoons peut-on réaliser une configuration avec (au moins) trois spins électroniques parallèles dans une sous couche 2p?
- Quel est l'élément le plus stable parmi ceux de la première période qui comporte des éléments du bloc p?
Que se passerait-il si l'électron avait un spin s=1?
- Combien de familles (groupes) comprendra
- Enumérez les valeurs possibles de
- Soit deux moments angulaires
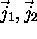 indépendants (avec
indépendants (avec 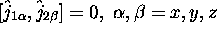 ) et leur somme
) et leur somme 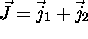 .
.
- Montrez que
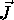 est aussi un moment angulaire.
est aussi un moment angulaire.
- Montrez que
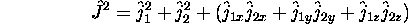
ne commute pas avec
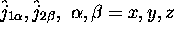 mais qu'il commute bien avec
mais qu'il commute bien avec 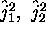 .
.
- Montrez que
- En utilisant l'exemple de la configuration
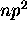 pour un atome, illustrez clairement la relation entre les concepts suivants:
pour un atome, illustrez clairement la relation entre les concepts suivants:
(a) configuration électronique, (b) termes spectraux, (c) états
- À l'aide d'un diagramme de niveaux d'énergie, illustrez l'effet Zeeman sur les états du terme
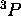 de la configuration
de la configuration 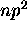 .
.
- Considérons la configuration
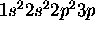 de l'azote dans un état excité. On montre que les états de plus basse d'energie dérivant de cette configuation forment un terme spectral
de l'azote dans un état excité. On montre que les états de plus basse d'energie dérivant de cette configuation forment un terme spectral 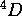 . D'autre part, on sait que la configuration
. D'autre part, on sait que la configuration 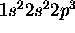 de l'état fondamental de l'atome ne peut pas donner un terme
de l'état fondamental de l'atome ne peut pas donner un terme 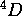 . Quel facteur interdit le terme
. Quel facteur interdit le terme 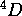 pour la configuration de l'état fondamental de l'azote? Expliquez pourquoi ce facteur n'opère plus dans le cas de la configuration
pour la configuration de l'état fondamental de l'azote? Expliquez pourquoi ce facteur n'opère plus dans le cas de la configuration 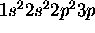 .
.
- Donnez les termes spectraux dérivant de la configuration
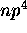 dans l'ordre des énergies croissantes (couplage spin-orbite inclus). Indiquez la dégénérescence de chaque niveau.
dans l'ordre des énergies croissantes (couplage spin-orbite inclus). Indiquez la dégénérescence de chaque niveau.
- Montrez que les termes spectraux dérivant d'une configuration
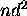 sont:
sont: 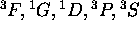 . Calculez les valeurs de J associées à chacun de ces termes.
. Calculez les valeurs de J associées à chacun de ces termes.
- La configuration de l'état fondamental de l'atome de Zirconium est
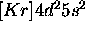 . Celle de l'atome de Nickel est
. Celle de l'atome de Nickel est 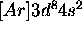 . Indiquez à quel terme spectral appartiendrait l'état fondamental dans chacun de ces deux cas.
. Indiquez à quel terme spectral appartiendrait l'état fondamental dans chacun de ces deux cas.
- La configuration de l'état fondamental de l'ion
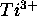 est
est

où
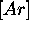 représente la configuration
représente la configuration 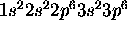 des électrons du `coeur' de l'atome. Grâce à l'effet d'écran de ces électrons de coeur, on peut considérer que l'électron d est assujetti à un champ moyen équivalent à celui d'un noyau de charge Z=+4. Dans cette approximation, l'ion
des électrons du `coeur' de l'atome. Grâce à l'effet d'écran de ces électrons de coeur, on peut considérer que l'électron d est assujetti à un champ moyen équivalent à celui d'un noyau de charge Z=+4. Dans cette approximation, l'ion 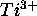 est donc considéré comme un atome hydrogénoïde exité à un état 3d.
est donc considéré comme un atome hydrogénoïde exité à un état 3d.
- Décrivez les termes spectraux que peut donner la configuration
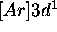 de l'ion
de l'ion 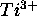 .
.
- Décrivez comment le niveau
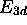 de l'ion se scinderait en plusieurs niveaux si l'on tient compte du couplage spin-orbite. Indiquez la dégénérescence de chaque niveau d'énergie dans ce schéma.
de l'ion se scinderait en plusieurs niveaux si l'on tient compte du couplage spin-orbite. Indiquez la dégénérescence de chaque niveau d'énergie dans ce schéma.
- Décrivez les termes spectraux que peut donner la configuration
