Nous avons vu que, dans le cadre d'un modèle des électrons indépendants, la fonction d'onde d'un système à plusieurs électrons, qu'il soit atomique ou moléculaire, est un produit antisymétrisé d'orbitales ou plutôt de spin-orbitales. Ce sont des fonctions mono-électroniques qui, dans le cas d'un atome, s'apparentent aux fonctions propres du système hydrogénoïde correspondant. De la même manière, on peut obtenir une idée qualitative de la forme et de la disposition des orbitales d'une molécule donnée en considérant le système à un électron correspondant. Dans ce qui suit, on considérera en détail la construction des orbitales des molécules diatomiques homo-nucléaires
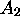, et hétéronucléaires AB. Le principe de la
classification des orbitales selon leur comportement vis-à-
vis des opérations de symétrie du système sera d'abord exposé.
La construction des orbitales selon une méthode courante, dite
méthode LCAO sera ensuite abordée. Les principes de cette méthode
seront ensuites utilisées dans la description des orbitales
moléculaires de quelques molécules simples.
Il est important de souligner que la structure électronique que l'on considère ici est associée à une configuration nucléaire ou géométrie donnée. Cette structure électronique, les orbitales, leur énergie, leur degré d'occupation, etc., varie d'une géométrie nucléaire à une autre. Quel sens peut-on donner à ce concept de structure électronique définie à une configuration nucléaire fixée? Quel rôle peuvent-ils jouer, les quantités comme l'énergie électronique totale ou orbitalaire, vis-à-vis des mouvements nucléaires? La réponse à ces questions est fournie par le formalisme sous-jacent à ce qui est appelé approximation de Born-Oppenheimer. Nous donnerons donc tout d'abord un survol de cette approximation.