



Next: Principe de la
Up: ORBITALES MOLÉCULAIRES
Previous: Molécules linéaires centrosymétriques
L'équation de Schrödinger indépendante du temps peut être résolue exactement dans un cas moléculaire simple, celui de l'ion moléculaire 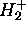 dans une géométrie nucléaire fixée correspondant à une valeur donnée de la distance internucléaire R. L'exposé de ces solutions exactes présente peu d'intérêt dans la mesure où ni ces solutions elles-même, ni leur mode de construction exacte ne sont généralisables à des système plus complexes.
dans une géométrie nucléaire fixée correspondant à une valeur donnée de la distance internucléaire R. L'exposé de ces solutions exactes présente peu d'intérêt dans la mesure où ni ces solutions elles-même, ni leur mode de construction exacte ne sont généralisables à des système plus complexes.
Il suffit de mentionner que l'étude des solutions exactes pour 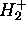 montre que ses
orbitales moléculaires tendent tous asymptotiquement, (c.à d. dans la limite
montre que ses
orbitales moléculaires tendent tous asymptotiquement, (c.à d. dans la limite 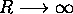 ),
vers des combinaisons linéaires simples d'orbitales atomiques. En
fait, ces combinaisons linéaires continuent à bien représenter,
dans une très bonne approximation, les orbitales de ce système
à un électron à tout
),
vers des combinaisons linéaires simples d'orbitales atomiques. En
fait, ces combinaisons linéaires continuent à bien représenter,
dans une très bonne approximation, les orbitales de ce système
à un électron à tout 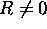 . Toute approche théorique dans
laquelle on exprime les orbitales moléculaires sous la forme de
combinaisons linéaires d'orbitales atomiques est désignée par le
vocable général de méthode LCAO (pour Linear Combination of Atomic
Orbitals), et constitue l'approche la plus couramment utilisée
dans des calculs de chimie quantique.
. Toute approche théorique dans
laquelle on exprime les orbitales moléculaires sous la forme de
combinaisons linéaires d'orbitales atomiques est désignée par le
vocable général de méthode LCAO (pour Linear Combination of Atomic
Orbitals), et constitue l'approche la plus couramment utilisée
dans des calculs de chimie quantique.
Cours WWW Intro a la Chimie Quantique
Sat Jan 13 22:02:54 EST 2001
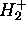 montre que ses
orbitales moléculaires tendent tous asymptotiquement, (c.à d. dans la limite
montre que ses
orbitales moléculaires tendent tous asymptotiquement, (c.à d. dans la limite 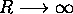 ),
vers des combinaisons linéaires simples d'orbitales atomiques. En
fait, ces combinaisons linéaires continuent à bien représenter,
dans une très bonne approximation, les orbitales de ce système
à un électron à tout
),
vers des combinaisons linéaires simples d'orbitales atomiques. En
fait, ces combinaisons linéaires continuent à bien représenter,
dans une très bonne approximation, les orbitales de ce système
à un électron à tout 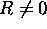 . Toute approche théorique dans
laquelle on exprime les orbitales moléculaires sous la forme de
combinaisons linéaires d'orbitales atomiques est désignée par le
vocable général de méthode LCAO (pour Linear Combination of Atomic
Orbitals), et constitue l'approche la plus couramment utilisée
dans des calculs de chimie quantique.
. Toute approche théorique dans
laquelle on exprime les orbitales moléculaires sous la forme de
combinaisons linéaires d'orbitales atomiques est désignée par le
vocable général de méthode LCAO (pour Linear Combination of Atomic
Orbitals), et constitue l'approche la plus couramment utilisée
dans des calculs de chimie quantique.
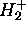 dans une géométrie nucléaire fixée correspondant à une valeur donnée de la distance internucléaire R. L'exposé de ces solutions exactes présente peu d'intérêt dans la mesure où ni ces solutions elles-même, ni leur mode de construction exacte ne sont généralisables à des système plus complexes.
dans une géométrie nucléaire fixée correspondant à une valeur donnée de la distance internucléaire R. L'exposé de ces solutions exactes présente peu d'intérêt dans la mesure où ni ces solutions elles-même, ni leur mode de construction exacte ne sont généralisables à des système plus complexes.