



Next: Méthode LCAO
Up: Symétrie des orbitales:
Previous: Généralités
Notons que la nomenclature du tableau 5.1 s'applique à
toute molécule linéaire. Dans le cas des molécules centrosymétriques, telles les molécules diatomiques homonucléaires 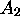 , des triatomiques XAX, etc.,
l'existence d'une symétrie d'inversion par rapport au centre de la
molécule permet la classification des orbitales selon leur
comportement vis-à-vis de cette inversion aussi. Les orbitales peuvent
être paires (de caractère g, pour gerade
, des triatomiques XAX, etc.,
l'existence d'une symétrie d'inversion par rapport au centre de la
molécule permet la classification des orbitales selon leur
comportement vis-à-vis de cette inversion aussi. Les orbitales peuvent
être paires (de caractère g, pour gerade 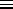 paire en
allemand) ou impaires (de caractère u, pour ungerade
paire en
allemand) ou impaires (de caractère u, pour ungerade 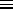 impaire en allemand). On est donc amené à parler d'orbitales
impaire en allemand). On est donc amené à parler d'orbitales
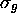 ,
, 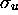 ,
, 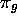 ,
, 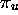 , etc
, etc . Les
caractéristiques généraux qu'on vient d'établir pour les
orbitales d'une molécule linéaire centrosymétrique sont appelés
symétrie de l'orbitale: on parle ainsi d'une orbitale de
symétrie
. Les
caractéristiques généraux qu'on vient d'établir pour les
orbitales d'une molécule linéaire centrosymétrique sont appelés
symétrie de l'orbitale: on parle ainsi d'une orbitale de
symétrie 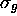 , par exemple.
, par exemple.
De façon plus générale, la classification des orbitales d'une molécule quelconque utilise les concepts de la théorie des groupes de symétrie . Chaque molécule peut être classée en terme de la symétrie que sa géométrie d'équilibre présente: par exemple,
. Chaque molécule peut être classée en terme de la symétrie que sa géométrie d'équilibre présente: par exemple, 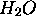 est de symétrie
est de symétrie 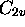 ,
, 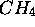 de symétrie
de symétrie 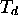 . Pour chaque groupe de symétrie donné, il existe un petit nombre de 'patrons' de comportement possibles de fonctions dites adaptées à la symétrie, c.à d. de fonctions propres communes aux différents opérateurs de symmétrie du groupe. Ces 'patrons' définissent des classes appelées représentations irréductibles du groupe. Les orbitales moléculaires (OM) et les états moléculaires, (ceux-ci sont représentés par des déterminants de Slater employant des OM), sont classés et identifiés en termes de ces représentations irréductibles de la théorie des groupes. L'utilisation systématique de la symétrie facilite aussi grandement la construction des OM par la méthode LCAO détaillée dans les sections à suivre.
. Pour chaque groupe de symétrie donné, il existe un petit nombre de 'patrons' de comportement possibles de fonctions dites adaptées à la symétrie, c.à d. de fonctions propres communes aux différents opérateurs de symmétrie du groupe. Ces 'patrons' définissent des classes appelées représentations irréductibles du groupe. Les orbitales moléculaires (OM) et les états moléculaires, (ceux-ci sont représentés par des déterminants de Slater employant des OM), sont classés et identifiés en termes de ces représentations irréductibles de la théorie des groupes. L'utilisation systématique de la symétrie facilite aussi grandement la construction des OM par la méthode LCAO détaillée dans les sections à suivre.
Cours WWW Intro a la Chimie Quantique
Sat Jan 13 22:02:54 EST 2001
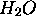 est de symétrie
est de symétrie 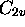 ,
, 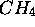 de symétrie
de symétrie 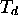 . Pour chaque groupe de symétrie donné, il existe un petit nombre de 'patrons' de comportement possibles de fonctions dites adaptées à la symétrie, c.à d. de fonctions propres communes aux différents opérateurs de symmétrie du groupe. Ces 'patrons' définissent des classes appelées représentations irréductibles du groupe. Les orbitales moléculaires (OM) et les états moléculaires, (ceux-ci sont représentés par des déterminants de Slater employant des OM), sont classés et identifiés en termes de ces représentations irréductibles de la théorie des groupes. L'utilisation systématique de la symétrie facilite aussi grandement la construction des OM par la méthode LCAO détaillée dans les sections à suivre.
. Pour chaque groupe de symétrie donné, il existe un petit nombre de 'patrons' de comportement possibles de fonctions dites adaptées à la symétrie, c.à d. de fonctions propres communes aux différents opérateurs de symmétrie du groupe. Ces 'patrons' définissent des classes appelées représentations irréductibles du groupe. Les orbitales moléculaires (OM) et les états moléculaires, (ceux-ci sont représentés par des déterminants de Slater employant des OM), sont classés et identifiés en termes de ces représentations irréductibles de la théorie des groupes. L'utilisation systématique de la symétrie facilite aussi grandement la construction des OM par la méthode LCAO détaillée dans les sections à suivre.
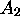 , des triatomiques XAX, etc.,
l'existence d'une symétrie d'inversion par rapport au centre de la
molécule permet la classification des orbitales selon leur
comportement vis-à-vis de cette inversion aussi. Les orbitales peuvent
être paires (de caractère g, pour gerade
, des triatomiques XAX, etc.,
l'existence d'une symétrie d'inversion par rapport au centre de la
molécule permet la classification des orbitales selon leur
comportement vis-à-vis de cette inversion aussi. Les orbitales peuvent
être paires (de caractère g, pour gerade 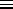 paire en
allemand) ou impaires (de caractère u, pour ungerade
paire en
allemand) ou impaires (de caractère u, pour ungerade 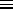 impaire en allemand). On est donc amené à parler d'orbitales
impaire en allemand). On est donc amené à parler d'orbitales
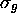 ,
, 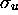 ,
, 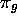 ,
, 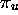 , etc
, etc . Les
caractéristiques généraux qu'on vient d'établir pour les
orbitales d'une molécule linéaire centrosymétrique sont appelés
symétrie de l'orbitale: on parle ainsi d'une orbitale de
symétrie
. Les
caractéristiques généraux qu'on vient d'établir pour les
orbitales d'une molécule linéaire centrosymétrique sont appelés
symétrie de l'orbitale: on parle ainsi d'une orbitale de
symétrie 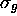 , par exemple.
, par exemple.