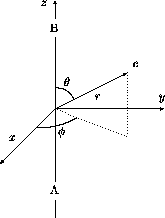
Figure 5.1: Définition des coordonnées sphériques pour un électron dans une molécule diatomique
Toute molécule diatomique, et plus généralement, toute molécule linéaire possède une symétrie de révolution autour de l'axe internucléaire, qui est un axe de rotation d'ordre infini. Ceci implique que les propriétés de cette molécule sont invariantes par rapport à une rotation d'un angle quelconque autour de cet axe. En utilisant les coordonnées sphériques définies à la figure 5.1, on trouve que
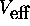 ainsi que
ainsi que 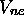 , le potentiel d'attraction coulombienne
électron-noyau, ne dépendent que de r et de
, le potentiel d'attraction coulombienne
électron-noyau, ne dépendent que de r et de 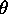 .
.

Figure 5.1: Définition des coordonnées sphériques pour un électron dans une
molécule diatomique
Par conséquent, on trouve que 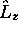 commute avec
commute avec 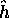 , et
les orbitales moléculaires peuvent être construites fonctions
propres de
, et
les orbitales moléculaires peuvent être construites fonctions
propres de 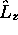 . En fait, l'hamiltonien mono-électronique
effectif
. En fait, l'hamiltonien mono-électronique
effectif 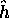 ne dépend de l'angle
ne dépend de l'angle 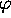 que par
l'intermédiaire de l'opérateur
que par
l'intermédiaire de l'opérateur 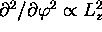 . Ses valeurs propres, c'est-à-dire les énergies
orbitalaires
. Ses valeurs propres, c'est-à-dire les énergies
orbitalaires 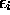 ne dépendent donc du nombre quantique
magnétique m qu'à travers
ne dépendent donc du nombre quantique
magnétique m qu'à travers 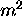 , c'est-à-dire à travers
, c'est-à-dire à travers
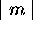 ; tout niveau caractérisé par une valeur k de
; tout niveau caractérisé par une valeur k de
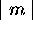 non nulle est donc doublement dégénéré, car l'on
trouve toujours deux orbitales qui y sont associées, l'une avec
m = +k, l'autre avec m = -k. On nomme les orbitales de la molécule,
selon la valeur de
non nulle est donc doublement dégénéré, car l'on
trouve toujours deux orbitales qui y sont associées, l'une avec
m = +k, l'autre avec m = -k. On nomme les orbitales de la molécule,
selon la valeur de 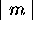 , par une lettre grecque minuscule en
utilisant la convention définie au tableau 5.1.
, par une lettre grecque minuscule en
utilisant la convention définie au tableau 5.1.

Table 5.1: Convention de nomenclature des orbitales d'une molécule linéaire