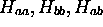 et
et 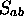 :
:
Pour des fins d'analyse qualitative de cette section, il est
commode d'admettre les hypothèses suivantes concernant les
intégrales 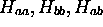 et
et 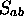 :
:
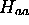 : Dans une première approximation,
on peut admettre que
: Dans une première approximation,
on peut admettre que
où 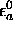 est l'énergie de l'orbitale
est l'énergie de l'orbitale 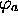 dans l'atome A,
dans l'atome A, 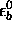 celle de l'orbitale
celle de l'orbitale
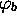 dans l'atome B. Ce sont des quantités négatives.
dans l'atome B. Ce sont des quantités négatives.
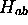 : On a estimé que cette intégrale peut
s'écrire soit sous la forme
: On a estimé que cette intégrale peut
s'écrire soit sous la forme
ou sous la forme
où 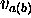 est, grosso-modo, l'énergie d'attraction moyenne ressenti, de la part du noyau
est, grosso-modo, l'énergie d'attraction moyenne ressenti, de la part du noyau 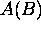 , par un
électron localisé dans le voisinage de ce noyau, et décrit par
l'orbitale atomique
, par un
électron localisé dans le voisinage de ce noyau, et décrit par
l'orbitale atomique 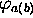 .
.
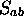 : La valeur absolue de cette
intégrale est toujours inférieure à 1;
: La valeur absolue de cette
intégrale est toujours inférieure à 1; 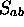 peut être
positive ou négative et dépend de la nature des deux orbitales
impliquées, ainsi que de leur orientation relative. La
figure 5.2 illustre quelques cas typiques.
peut être
positive ou négative et dépend de la nature des deux orbitales
impliquées, ainsi que de leur orientation relative. La
figure 5.2 illustre quelques cas typiques.
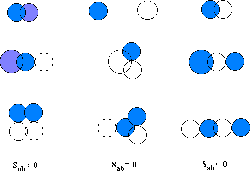
Figure: Illustration de la dépendance de 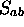 sur la nature et l'orientation
relative des deux orbitales impliquées
sur la nature et l'orientation
relative des deux orbitales impliquées
Dans ce cas, on a 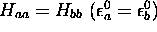 par symétrie.
par symétrie.
L'équation séculaire donne
Si l'on suppose que 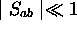 , ce qui est souvent
valide, on peut développer en série de puissance de
, ce qui est souvent
valide, on peut développer en série de puissance de 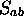 pour
obtenir
pour
obtenir
de sorte que, quel que soit le signe de 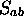 , la différence
d'énergie entre le niveau moléculaire le plus haut (orbitale
antiliante) et le niveau atomique est supérieure à celle entre le
niveau moléculaire le plus bas (orbitale liante) et le niveau
atomique:
, la différence
d'énergie entre le niveau moléculaire le plus haut (orbitale
antiliante) et le niveau atomique est supérieure à celle entre le
niveau moléculaire le plus bas (orbitale liante) et le niveau
atomique:
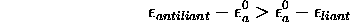
Correspondant à 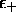 , (5.23), on obtient,
du système (5.17)
, (5.23), on obtient,
du système (5.17)
la dernière égalité provenant de la condition de normalisation
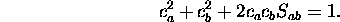
De même, pour 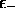 , on obtient
, on obtient
Pour fixer les idées, considérons le cas spécifique
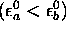 .
.
Écrivons explicitement l'équation séculaire, (5.18), sous forme développée, utilisant (5.19)
Le discriminant de cette équation quadratique peut s'écrire
Or, d'après (5.21) et (5.22), 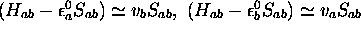 , de sorte que le second terme
entre accolades dans cette expression de
, de sorte que le second terme
entre accolades dans cette expression de 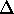 est du second
ordre en
est du second
ordre en 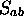 . On peut donc écrire
. On peut donc écrire
à cet ordre. On obtient alors, au second ordre en 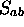
et
On voit donc que  , c'est-à-dire que
, c'est-à-dire que
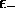 est le niveau orbitalaire le plus bas. Ce niveau
moléculaire le plus bas,
est le niveau orbitalaire le plus bas. Ce niveau
moléculaire le plus bas, 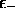 , est plus profond que le
plus bas des deux niveaux atomiques. Un électron occupant ce niveau
stabilisera donc la molécule. Par contre, le niveau moléculaire
, est plus profond que le
plus bas des deux niveaux atomiques. Un électron occupant ce niveau
stabilisera donc la molécule. Par contre, le niveau moléculaire
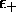 est supérieur au niveau atomique le plus élevé,
et un électron occupant
est supérieur au niveau atomique le plus élevé,
et un électron occupant 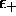 déstabilisera la molécule.
Finalement on remarque que l'écart entre le niveau moléculaire
déstabilisera la molécule.
Finalement on remarque que l'écart entre le niveau moléculaire
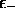 et le niveau atomique le plus bas
et le niveau atomique le plus bas 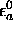 est d'autant plus faible que les deux niveaux atomiques de départ
sont plus éloignés.
est d'autant plus faible que les deux niveaux atomiques de départ
sont plus éloignés.
Correspondant à 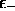 , (5.31), on a
, (5.31), on a
Posant

et nous rappelant que 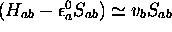 , nous pouvons ré-écrire (5.33) sous
la forme
, nous pouvons ré-écrire (5.33) sous
la forme
qui, avec la condition de normalisation
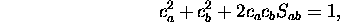
donne
au second ordre en 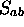 (t en est du premier ordre).
(t en est du premier ordre).
On a donc, pour l'orbitale moléculaire de plus basse énergie
(énergie orbitalaire 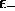 )
)
Un calcul analogue commencant avec la substitution 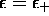 dans le système (5.17), donne
dans le système (5.17), donne
où

Dans 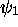 , on a
, on a 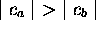 , et
l'orbitale
, et
l'orbitale 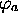 , dont l'énergie est la plus proche de
, dont l'énergie est la plus proche de
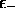 , domine l'orbitale atomique
, domine l'orbitale atomique 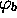 ; de même,
dans
; de même,
dans 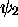 ,
, 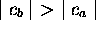 , et l'orbitale
atomique
, et l'orbitale
atomique 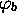 domine l'orbitale
domine l'orbitale 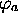 . Dans le cas
limite
. Dans le cas
limite 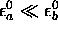 ,
, 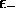 est
virtuellement confondue avec
est
virtuellement confondue avec 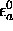 et
et 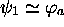 , tandis que
, tandis que 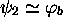 , avec
, avec
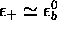 .
.
Les observations précédentes ne se limitent pas à un développement LCAO limité à deux termes, comme celui de (5.11). Elles se généralisent pour donner les règles simples suivantes gouvernant tout développement LCAO:
Plus ces deux facteurs sont importants, mieux se ferait le mélange
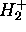 , tous les orbitales
, tous les orbitales 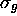 ,
,
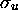 , etc, décrites précédemment sont adaptées à
la symétrie de cette molécule.
, etc, décrites précédemment sont adaptées à
la symétrie de cette molécule.