
Pour exposer simplement le principe de la méthode LCAO, nous considérerons l'approche la plus élémentaire de ce type pour une molécule diatomique. Dans cette approche, on écrit les orbitales d'une molécule AB sous la forme générale
où 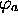 et
et 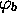 sont des orbitales atomiques
centrées sur le noyau A et B, respectivement, et sont supposées
connues. Les coefficients
sont des orbitales atomiques
centrées sur le noyau A et B, respectivement, et sont supposées
connues. Les coefficients 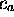 et
et 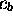 sont les inconnues du
problème, et sont déterminés variationnellement. L'exposé suivant
utilise l'hypothèse que les orbitales atomiques
sont les inconnues du
problème, et sont déterminés variationnellement. L'exposé suivant
utilise l'hypothèse que les orbitales atomiques 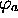 et
et
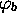 sont choisies réelles, ainsi que le sont les coefficients
sont choisies réelles, ainsi que le sont les coefficients
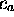 et
et 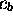 . L'application du théorème variationnel (voir Chapitre 1, section 1.3.3) demande
que l'on minimise la quantité
. L'application du théorème variationnel (voir Chapitre 1, section 1.3.3) demande
que l'on minimise la quantité 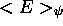 , définie par
, définie par
par rapport à 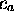 et
et 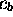 (Le dénominateur représente la
constante de normalisation de la fonction
(Le dénominateur représente la
constante de normalisation de la fonction 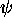 ). L'équation (5.12)
représente, dans l'approximation des électrons indépendants,
l'énergie mono-électronique moyenne dans l'orbitale d'essai
). L'équation (5.12)
représente, dans l'approximation des électrons indépendants,
l'énergie mono-électronique moyenne dans l'orbitale d'essai 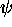 .
Avec (5.11), on a
.
Avec (5.11), on a
où
et
Notons que l'intégrale 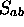 n'est pas nulle: deux orbitales
atomiques centrées sur des noyaux différents ne sont pas
orthogonales. Cette intégrale s'appelle le recouvrement des
orbitales
n'est pas nulle: deux orbitales
atomiques centrées sur des noyaux différents ne sont pas
orthogonales. Cette intégrale s'appelle le recouvrement des
orbitales 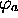 et
et 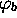 . Les intégrales
. Les intégrales 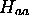 ,
,
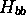 et
et 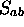 ne dépendent que des fonctions connues
ne dépendent que des fonctions connues
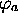 et
et 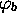 . Ce sont donc des quantités que
l'on peut considérer comme connues. Elles dépendent bien entendu
de R. Minimisant
. Ce sont donc des quantités que
l'on peut considérer comme connues. Elles dépendent bien entendu
de R. Minimisant 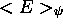 par rapport à
par rapport à 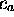 et
et 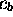 , on
obtient
, on
obtient
qui est un système d'équations linéaires pour les deux inconnues
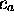 et
et 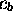 . Ce système ne possède de solutions non-
triviales que si et seulement si
. Ce système ne possède de solutions non-
triviales que si et seulement si
Cette condition, appelée équation séculaire, représente une
équation algébrique du second ordre pour l'énergie  , qui
elle aussi, était inconnue. Elle possède deux solutions,
, qui
elle aussi, était inconnue. Elle possède deux solutions,
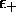 et
et 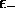 , et l'on ne peut obtenir que deux
orbitales moléculaires avec une combinaison linéaire de la forme
limitée de (5.11). La forme de ces deux orbitales s'obtient
une fois que les coefficients
, et l'on ne peut obtenir que deux
orbitales moléculaires avec une combinaison linéaire de la forme
limitée de (5.11). La forme de ces deux orbitales s'obtient
une fois que les coefficients 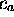 et
et 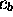 sont tirés du
système (5.17), avec
sont tirés du
système (5.17), avec 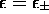 .
.