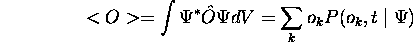
On a vu, lors de la démonstration de l'équivalence des deux formes du postulat 5, que
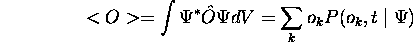
dans tout état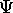 
(voir (1.15)
Dans le cas particulier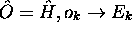 
et
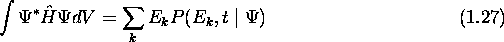
Soit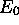 
, l'énergie de l'état fondamental du système, alors
ce qui implique que
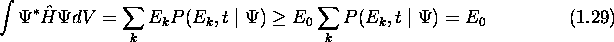
comme les quantités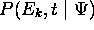 
sont positives et leur
somme vaut exactement 1.
On obtient ainsi un résultat général que l'on peut énoncer sous forme de théorème:
Théorème variationnel:
la valeur moyenne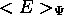 
de l'énergie dans tout état 
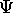est toujours supérieure à
l'énergie de l'état fondamental du système.
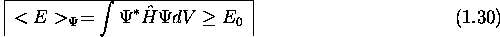
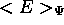ne peut égaler 
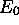que si 
,
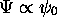c.à.d. qu'elle représente exactement l'état fondamental du
système.
En imaginant un balayage de l'espace des états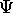 
, on voit donc
que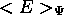 
atteint un minimum absolu en 
.
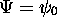Le théorème qu'on vient d'énoncer traduit donc un principe
variationel, et il est à la base des procédures de détermination
approchée de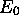 
et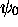 
par minimalisation de 
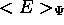dans une classe restreinte de fonctions 
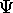, qui sont alors
appellées fonctions d'essai. Ces procédures sont surtout utiles
dans le cas où la détermination de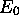 
et 
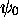par une
méthode de résolution directe de l'équation de Schrödinger
indépendante du temps s'avère difficile ou impossible.