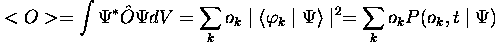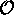 , quand le
système se trouve dans l'état décrit par
, quand le
système se trouve dans l'état décrit par 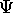 , est donnée par
, est donnée par
La valeur moyenne d'une propriété physique 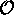 , quand le
système se trouve dans l'état décrit par
, quand le
système se trouve dans l'état décrit par 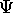 , est donnée par
, est donnée par

ou, plus simplement
si la fonction d'état 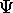 est bien normée, c.à.d. si
est bien normée, c.à.d. si

Toujours dans l'hypothèse que la fonction d'état 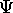 est
normée, une expression équivalente du postulat 5 est:
La probabilité de trouver la valeur propre
est
normée, une expression équivalente du postulat 5 est:
La probabilité de trouver la valeur propre 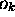 (de l'opérateur
hermitique
(de l'opérateur
hermitique 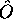 ), lors d'une mesure de la propriété
), lors d'une mesure de la propriété 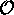 effectuée au temps t sur le système quantique préparé dans
l'état décrit par
effectuée au temps t sur le système quantique préparé dans
l'état décrit par 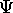 , est donnée par le carré du module de
la projection de la fonction d'état
, est donnée par le carré du module de
la projection de la fonction d'état 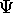 sur la fonction propre
sur la fonction propre
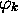 associée à la valeur propre
associée à la valeur propre 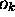 :
:
où la projection 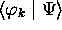 est définie
par
est définie
par
et il était supposé que les fonctions propres 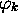 sont
orthonormées.
sont
orthonormées.
Interprétation:
Pour appréhender ce postulat, il est utile d'imaginer un très
grand nombre de répliques identiques du système, préparées toutes
dans le même état initial, 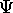 . Selon le postulat 4, la
mesure de
. Selon le postulat 4, la
mesure de 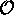 sur chacune des répliques, produira une valeur de
sur chacune des répliques, produira une valeur de
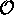 qui est précisément une des valeurs propres
qui est précisément une des valeurs propres 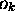 .
Cependant à priori, on ne peut pas prédire laquelle de ces valeurs
propres sera obtenu lors de la mesure effectuée sur une réplique
donnée, et l'ensemble des résultats revêt un caractère
statistique. Selon le cas, la distribution statistique des résultats
de mesure de
.
Cependant à priori, on ne peut pas prédire laquelle de ces valeurs
propres sera obtenu lors de la mesure effectuée sur une réplique
donnée, et l'ensemble des résultats revêt un caractère
statistique. Selon le cas, la distribution statistique des résultats
de mesure de 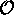 aura les caractéristiques suivants
aura les caractéristiques suivants
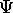 est une fonction propre (elle décrit un état
propre) de
est une fonction propre (elle décrit un état
propre) de 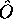 associée à la valeur propre
associée à la valeur propre 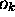 ,
c.à.d.
,
c.à.d.

alors des mesures répétées de 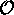 donnent
donnent 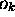 toujours. Cette valeur serait donc observée avec certitude.
toujours. Cette valeur serait donc observée avec certitude.
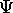 n'est pas une fonction propre de
n'est pas une fonction propre de 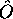 alors les
mesures répétées de
alors les
mesures répétées de 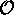 donnent chaque fois une valeur
propre
donnent chaque fois une valeur
propre 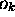 différente: La mesure met le système dans l'état
propre
différente: La mesure met le système dans l'état
propre 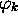 de
de 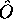 associé à la valeur propre
associé à la valeur propre
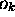 observée. Chaque valeur propre
observée. Chaque valeur propre 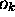 a une probabilité
d'être observée qui est donnée par (1.13).
La valeur moyenne de
a une probabilité
d'être observée qui est donnée par (1.13).
La valeur moyenne de 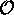 est
est
Démonstration:
L'équivalence des deux formes du postulat 5, exprimée par
(1.15), se démontre de la façon suivante: on sait
que 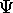 peut être développée sur la base orthonormée des
fonctions propres
peut être développée sur la base orthonormée des
fonctions propres 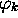 de
de 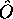 . On a ainsi
. On a ainsi
Montrons d'abord que les coefficients 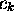 sont données par les
'projections' de (1.14). En effet
sont données par les
'projections' de (1.14). En effet
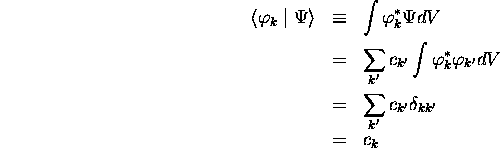
En passant de la deuxième à la troisième ligne, on a utilisé
l'orthonormalité des 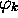 . À cause du
. À cause du 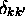 (
(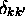 vaut 0 si
vaut 0 si 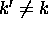 et 1 si
et 1 si 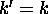 ) qu'elle contient,
la somme sur
) qu'elle contient,
la somme sur 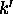 se réduit à un seul terme,
se réduit à un seul terme, 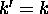 . On a donc bien
. On a donc bien
Substituons maintenant ce développement de 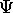 , (1.16)
, dans (1.12); on obtient
, (1.16)
, dans (1.12); on obtient
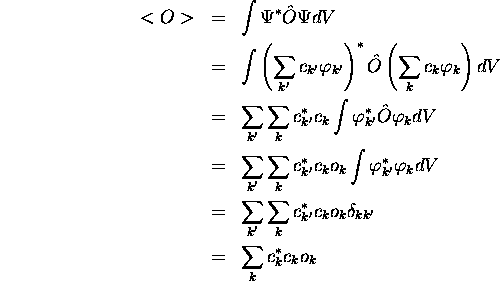
Finalement, rappelant (1.17), on obtient