



Next: Théorème variationnel
Up: Conséquences des postulats
Previous: Propriétés des états
Il est clair que deux grandeurs physiques A et B ne sont mesurables
simultanément, ou compatibles que si la détermination
précise de l'une n'empêche pas celle de l'autre. Ceci signifie que les
fonctions propres de 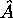 doivent aussi être fonctions propres de
doivent aussi être fonctions propres de
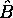 . Par conséquent, les deux grandeurs physiques A et B ne sont
compatibles que si les opérateurs qui leur sont associés admettent des
fonctions propres communes. On montre que la condition nécessaire
et suffisante pour que ceci soit possible est que
. Par conséquent, les deux grandeurs physiques A et B ne sont
compatibles que si les opérateurs qui leur sont associés admettent des
fonctions propres communes. On montre que la condition nécessaire
et suffisante pour que ceci soit possible est que 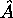 et
et 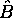 commutent:
commutent:

Exemples:
- x et
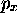 ne sont pas compatibles, à cause de la relation
de commutation fondamentale, (1.9). Par contre, y
et
ne sont pas compatibles, à cause de la relation
de commutation fondamentale, (1.9). Par contre, y
et 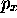 sont compatibles, toujours selon (1.9).
sont compatibles, toujours selon (1.9).
- Les trois composantes
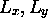 et
et 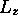 ne sont pas
compatibles; en effet, on peut montrer que
ne sont pas
compatibles; en effet, on peut montrer que



- Par contre, l'opérateur

associé à la propriété 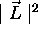 (carré de
la longueur du moment cinétique) commute avec n'importe quelle
composante de
(carré de
la longueur du moment cinétique) commute avec n'importe quelle
composante de 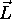 :
:
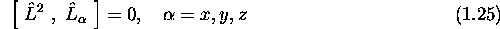
On peut donc déterminer simultanément la longueur de
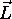 et une et une seule de ses composantes.
et une et une seule de ses composantes.
Dans le contexte de la chimie quantique, où l'on s'intéresse
aux états stationnaires des molécules, états d'énergie E
précise, rappelons-le, il est important et utile d'établir les
propriétés qui sont mutuellement compatibles et compatibles avec E.
Ce sont des constantes de mouvement. Les états stationnaires
sont complètement et uniquement spécifiés par la donnée des
valeurs propres de 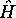 et des opérateurs associés à ces
constantes de mouvement. Très souvent, ces propriétés dénotent
l'invariance du système dans certaines opérations de symétrie.
et des opérateurs associés à ces
constantes de mouvement. Très souvent, ces propriétés dénotent
l'invariance du système dans certaines opérations de symétrie.
Exemples:
- L'électron de l'atome d'hydrogène sent un potentiel de
symétrie sphérique,
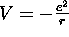 (écrit en c.g.s.
pour simplifier); son hamiltonien
(écrit en c.g.s.
pour simplifier); son hamiltonien

commute avec 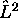 et
et 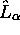 ,
, 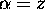 par
exemple (n'importe quelle composante conviendrait). Le système admet
donc deux constantes de mouvement, soit la longueur de
par
exemple (n'importe quelle composante conviendrait). Le système admet
donc deux constantes de mouvement, soit la longueur de 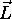 et
une de ses composantes,
et
une de ses composantes, 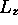 . Les états stationnaires de l'atome
sont ainsi spécifiés par trois nombres quantiques, n, l, m,
associés à E,
. Les états stationnaires de l'atome
sont ainsi spécifiés par trois nombres quantiques, n, l, m,
associés à E, 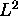 et
et 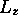 selon
selon

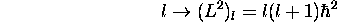

(On verra ces résultats en plus grands détails au Chapitre 3)
- L'électron dans
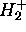 voit un potentiel de symétrie
cylindrique. La composante
voit un potentiel de symétrie
cylindrique. La composante 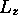 du moment cinétique
électronique le long de l'axe internucléaire (axe des z) est
conservée. En plus, l'invariance du potentiel dans l'opération
d'inversion
du moment cinétique
électronique le long de l'axe internucléaire (axe des z) est
conservée. En plus, l'invariance du potentiel dans l'opération
d'inversion 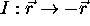 , par rapport au centre de l'axe
internucléaire (identifié ici comme l'origine des coordonnées)
permet la classification des états stationnaires selon leur
caractère de symétrie par rapport à cette opération. Par
exemple, l'état
, par rapport au centre de l'axe
internucléaire (identifié ici comme l'origine des coordonnées)
permet la classification des états stationnaires selon leur
caractère de symétrie par rapport à cette opération. Par
exemple, l'état
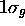
est l'état de plus basse énergie ayant 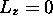 (premier état
du type
(premier état
du type 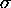 ), et de symétrie paire par rapport à l'inversion.
), et de symétrie paire par rapport à l'inversion.




Next: Théorème variationnel
Up: Conséquences des postulats
Previous: Propriétés des états
Cours WWW Intro a la Chimie Quantique
Sat Jan 13 22:02:54 EST 2001
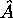 doivent aussi être fonctions propres de
doivent aussi être fonctions propres de
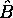 . Par conséquent, les deux grandeurs physiques A et B ne sont
compatibles que si les opérateurs qui leur sont associés admettent des
fonctions propres communes. On montre que la condition nécessaire
et suffisante pour que ceci soit possible est que
. Par conséquent, les deux grandeurs physiques A et B ne sont
compatibles que si les opérateurs qui leur sont associés admettent des
fonctions propres communes. On montre que la condition nécessaire
et suffisante pour que ceci soit possible est que 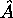 et
et 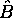 commutent:
commutent:

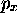 ne sont pas compatibles, à cause de la relation
de commutation fondamentale, (
ne sont pas compatibles, à cause de la relation
de commutation fondamentale, (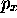 sont compatibles, toujours selon (
sont compatibles, toujours selon (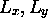 et
et 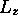 ne sont pas
compatibles; en effet, on peut montrer que
ne sont pas
compatibles; en effet, on peut montrer que




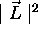 (carré de
la longueur du moment cinétique) commute avec n'importe quelle
composante de
(carré de
la longueur du moment cinétique) commute avec n'importe quelle
composante de 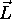 :
:
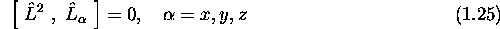
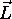 et une et une seule de ses composantes.
et une et une seule de ses composantes.
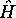 et des opérateurs associés à ces
constantes de mouvement. Très souvent, ces propriétés dénotent
l'invariance du système dans certaines opérations de symétrie.
et des opérateurs associés à ces
constantes de mouvement. Très souvent, ces propriétés dénotent
l'invariance du système dans certaines opérations de symétrie.
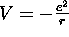 (écrit en c.g.s.
pour simplifier); son hamiltonien
(écrit en c.g.s.
pour simplifier); son hamiltonien

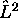 et
et 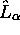 ,
, 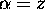 par
exemple (n'importe quelle composante conviendrait). Le système admet
donc deux constantes de mouvement, soit la longueur de
par
exemple (n'importe quelle composante conviendrait). Le système admet
donc deux constantes de mouvement, soit la longueur de 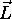 et
une de ses composantes,
et
une de ses composantes, 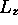 . Les états stationnaires de l'atome
sont ainsi spécifiés par trois nombres quantiques, n, l, m,
associés à E,
. Les états stationnaires de l'atome
sont ainsi spécifiés par trois nombres quantiques, n, l, m,
associés à E, 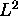 et
et 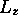 selon
selon

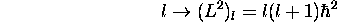

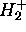 voit un potentiel de symétrie
cylindrique. La composante
voit un potentiel de symétrie
cylindrique. La composante 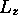 du moment cinétique
électronique le long de l'axe internucléaire (axe des z) est
conservée. En plus, l'invariance du potentiel dans l'opération
d'inversion
du moment cinétique
électronique le long de l'axe internucléaire (axe des z) est
conservée. En plus, l'invariance du potentiel dans l'opération
d'inversion 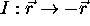 , par rapport au centre de l'axe
internucléaire (identifié ici comme l'origine des coordonnées)
permet la classification des états stationnaires selon leur
caractère de symétrie par rapport à cette opération. Par
exemple, l'état
, par rapport au centre de l'axe
internucléaire (identifié ici comme l'origine des coordonnées)
permet la classification des états stationnaires selon leur
caractère de symétrie par rapport à cette opération. Par
exemple, l'état
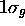
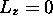 (premier état
du type
(premier état
du type 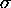 ), et de symétrie paire par rapport à l'inversion.
), et de symétrie paire par rapport à l'inversion.