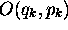 du système correspond un
opérateur linéaire hermitique
du système correspond un
opérateur linéaire hermitique 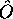 construit selon la
règle de correspondance suivante:
construit selon la
règle de correspondance suivante:
A chaque propriété physique, 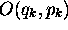 du système correspond un
opérateur linéaire hermitique
du système correspond un
opérateur linéaire hermitique 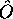 construit selon la
règle de correspondance suivante:
construit selon la
règle de correspondance suivante:

Comme cet opérateur est multiplicatif (multiplication par 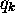 ), on
l'écrit souvent sans l'accent circonflexe, confondant l'opérateur
), on
l'écrit souvent sans l'accent circonflexe, confondant l'opérateur
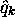 avec la variable
avec la variable 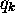 .
.

Les opérateurs 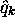 et
et 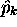 ne sont pas commutatifs.
En fait, ils obéissent à la relation de commutation suivante
ne sont pas commutatifs.
En fait, ils obéissent à la relation de commutation suivante
où 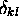 , le symbole de Kronecker, vaut 0 si
, le symbole de Kronecker, vaut 0 si 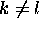 et 1 dans le cas contraire.
et 1 dans le cas contraire.
L'opérateur, 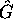 , associé à une grandeur physique G,
s'obtient en substituant dans l'expression classique,
, associé à une grandeur physique G,
s'obtient en substituant dans l'expression classique, 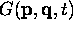 , de la grandeur les coordonnées
, de la grandeur les coordonnées 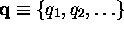 et les impulsions
et les impulsions 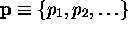 par les opérateurs hermitiques correspondants. On prendra soin de
rendre symétrique l'expression obtenu pour assurer que
par les opérateurs hermitiques correspondants. On prendra soin de
rendre symétrique l'expression obtenu pour assurer que 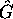 soit bien
hermitique.
soit bien
hermitique.
Exemples:
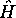 , (1.3), est l'opérateur
associé à la propriété ''énergie''
, (1.3), est l'opérateur
associé à la propriété ''énergie''
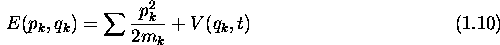
En effet, l'opérateur associé à E est
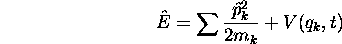
On vérifie aisément que ceci est hermitique, vue l'hermiticité
des opérateurs 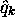 et
et 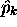 . Or
. Or
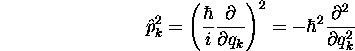
ce qui implique
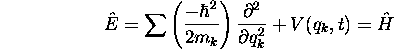
l'opérateur associé à la grandeur 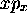 est
est

et non

car les deux opérateurs hermitiques x et 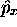 n'étant
pas commutatifs, le produit
n'étant
pas commutatifs, le produit 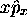 n'est pas hermitique.
n'est pas hermitique.
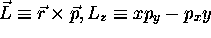 , est simplement
, est simplement

car 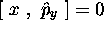 et
et 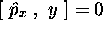 ;
les deux produits
;
les deux produits 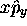 et
et 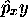 sont donc
hermitiques, ainsi que leur somme ou différence.
sont donc
hermitiques, ainsi que leur somme ou différence.