Si le système n'est pas perturbé, l'évolution de son état est gouvernée par l'équation de Schrödinger dépendante du temps
où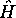 
est l'opérateur suivant, appellé hamiltonien du
système:
Remarque:
On note que l'équation de Schrödinger (1.2) est du premier ordre par rapport au temps: en dépit d'une ancienne terminologie, ce n'est pas une équation d'onde. Elle décrit un développement temporel déterministe de l'état quantique: si la fonction d'état,, est connue au temps
, alors elle est déterminée de façon non-ambiguë à tout temps ultérieur,
. Que la fonction d'état,
, elle même admet une interprétation probabiliste (selon le postulat 1) n'implique aucunement que la mécanique quantique soit non-déterministe.
États stationaires:
Dans le cas où le potentiel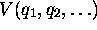 
est
indépendant du temps, correspondant à un système conservatif
en mécanique classique, il existe un ensemble de solutions
particulières à l'équation de Schrödinger (1.2) qui sont
de la forme
avec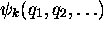 
indépendante du temps et
satisfaisant
c.à.d.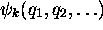 
est une fonction propre de
l'hamiltonien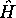 
avec valeur propre 
.
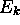Ces solutions particulières décrivent des états spéciaux appelés états stationaires. L'équation aux valeurs propres (1.5) est souvent appellée équation de Schrödinger indépendante du temps. Elle définit les états stationaires et n'a un sens que si le système est conservatif.
Toujours dans le cas d'un système conservatif, un état
quelconque, décrit par une solution générale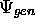 
de
l'équation de Schrödinger (1.2), peut être développé
en termes des états stationaires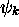 
, selon
Les coefficients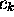 
dans ce développement sont indépendants du
temps et sont déterminés de façon non-équivoque par l'état
initial.
C'est surtout l'équation de Schrödinger indépendante du temps, (1.5), qui concerne la chimie quantique: on cherche en effet à obtenir les fonctions d'onde décrivant les états stationaires, et surtout l'état de plus basse énergie, l'état fondamental, des atomes et des molécules. Les transitions observées en spectroscopie s'effectuent entre ces états stationaires; leur détermination est donc un prérequis pour l'étude de la spectroscopie. Cependant il faut bien se rappeler que c'est l'équation de Schrödinger dépendante du temps, (1.2), qui est l'équation fondamentale de la mécanique quantique: elle joue le même rôle que l'équation de Newton en mécanique classique, soit celui d'une équation de mouvement.
