La perturbation d'une molécule par un champ électromagnétique externe faible permet de sonder la structure de cette molécule, c.à d. ses états stationnaires. Considérons par exemple l'action d'un champ électrique oscillant
sur la molécule. Elle se traduit par l'ajout, à l'hamiltonien, d'un potentiel d'interaction
où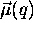 
représente le moment dipolaire de la molécule; on l'avait écrit comme une certaine fonction des coordonnées moléculaires, indiquées collectivement par q.
Le nouvel hamiltonien est
où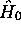 
décrit la molécule libre. L'hamiltonien 
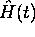dépend maintenant explicitement du temps, et la molécule perturbée devient un système non conservatif qui, en soi, ne possède pas d'état stationnaire. Cependant, on peut toujours développer une solution quelconque 
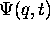, de l'équation de Schrödinger (dépendante du temps, bien entendu), sur la base complète et orthonormale des états propres de 
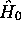, c.à d., des états stationnaires de la molécule libre.
On a déjà rencontré ce type de développement à l'équation (1.6). La différence est qu'ici, les coefficients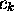 
dépendent de t. En fait, substituant le développement de (1.33) dans l'équation de Schrödinger (1.2), notant que, par définition, 
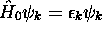avec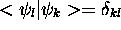 
, on obtient, après quelques manipulations mathématiques, un ensemble d'équations couplées pour les 
:
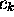Le développement précédent est surtout utile quand l'on part d'un état propre,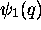 
de la molécule libre et quand le champ est suffisamment faible pour que l'on puisse supposer qu'en tout temps (durant l'action du rayonnement externe), l'état 
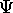reste très proche de 
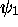, c.à d.,
Notons que (1.35) ne décrit qu'une première approximation (on l'appelle ' approximation d'ordre zéro'). En seconde approximation ( approximation d'ordre 1), on obtient les coefficients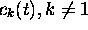 
, en substituant (1.35) au membre de droite de (1.34), qui devient alors,
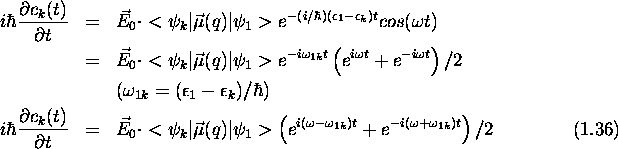
Intégrant les deux membres de cette dernière équation de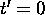 
à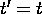 
, on obtient
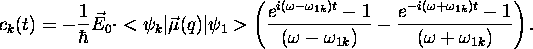
Il est commode de réécrire ce résultat sous la forme finale suivante:
où l'on a défini
Selon le postulat 5, la probabilité de trouver, au temps t, le système avec une énergie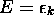 
, c.à d. dans l'état 
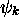, est
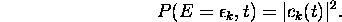
Cette probabilité est aussi la probabilité que le système effectue la transition de l'état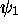 
à l'état 
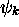sous l'action du champ. Avec le résultat final de (1.37 ), on peut écrire cette probabilité de transition sous la forme
On peut déjà tirer deux observations importantes:
) montre le graphe des 
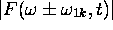vues comme fonctions de 
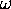, la fréquence de l'onde électromagnétique incidente, pour une valeur de t fixée et pour une fréquence de transition 
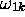positive. On voit clairement que, dans ce cas, le facteur 
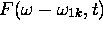domine largement 
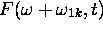, dans la région des valeurs physiques (valeurs positives) de 
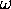. On peut donc écrire, pour 
,
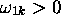En outre, la fonction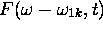 
est fortement localisée au voisinage de 
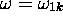, la localisation devenant de plus en plus accentuée pour des valeurs de t croissantes. À la limite 
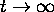, on peut dire que la transition 
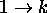ne peut se produire que si 
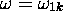exactement. C'est la fameuse condition de résonance de Bohr: De la radiation ne peut-être émise (ou absorbée, dans le cas 
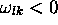) que si sa fréquence correspond exactement à la fréquence de transition.
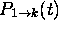est proportionnelle au carré du module de l'intégrale
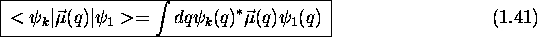
appellée moment de transition, pour la transition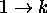 
. Dépendant de la symétrie du système considéré, cette intégrale n'est généralement non-nulle que si certaines conditions sont remplies. Elles sont appellées règles de sélection. On verra dans les chapitres suivants des exemples concrets de telles règles de sélection.
