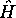Exercices

1. Vérifiez que la fonction définie par les équations (1.4) et (1.5) est en effet une solution de l'équation de Schrödinger (1.2).

2. Donnez un exemple de système non-conservatif.

3. Vérifiez que le second membre de (1.6) satisfait bien l'équation de Schrödinger (1.2).

4. Les fonctions propres de peuvent toujours être construites orthonormées, dans le sens qu'elles satisfont

   

   où 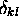vaut 1 si k = l et zéro dans le cas contraire. En utilisant cette donnée, montrez que les coefficients 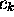de (1.6) sont déterminés par

   

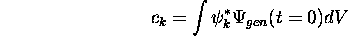
   où 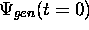décrit l'état initial au temps t = 0.

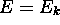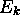5. En utilisant (1.6), et les résultats de l'exercice précédent, montrez que, même si un système conservatif n'est pas dans un état stationnaire, la probabilité qu'il possède une énergie , étant une valeur propre de l'hamiltonien 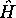, est indépendant du temps.

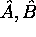6. (*) Soit deux opérateurs hermitique commutatifs, c.à d.

   

   Soit a une valeur propre non-dégénérée de 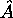, c. à d. qu'il n'existe, à une constante multplicative près, qu'une seule fonction 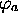satisfaisant

   

   Montrez que 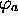est alors nécessairement fonction propre de .

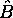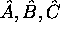7. (*) Montrez les identités mathématiques suivantes ( sont des opérateurs , 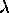est une constante):
   1. ,
   2. ,
   3. ,
   4. .
8. (*) Les trois composantes du vecteur moment cinétique sont

   

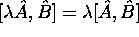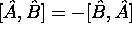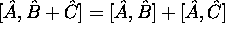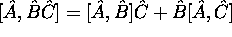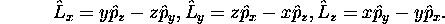
   En utilisant les résultats de l'exercice précédent, et en se rappelant les relations de commutation fondamentales, (1.9), démontrez la relation de commutation

   

9. (*) en admettant les relations de commutation cycliques, ()-(), démontrez que

   

   où 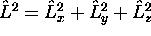.