



Next: Symétrie des orbitales:
Up: Approximation de Born-Oppenheimer
Previous: Hamiltonien moléculaire
On prendra soin de noter que, à cause de la
dépendance de 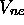 sur
sur 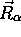 , l' hamiltonien
électronique
, l' hamiltonien
électronique 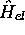 dépend
paramétriquement des coordonnées nucléaires. Il ne commute donc
pas avec l'opérateur
dépend
paramétriquement des coordonnées nucléaires. Il ne commute donc
pas avec l'opérateur 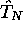 , et comme ces deux opérateurs
apparaissent dans l'hamiltonien moléculaire
, et comme ces deux opérateurs
apparaissent dans l'hamiltonien moléculaire 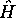 , les mouvements
électroniques et nucléaires ne sont pas séparables, c'est-à-
dire que, rigoureusement, on ne peut pas écrire la fonction
d'onde totale
, les mouvements
électroniques et nucléaires ne sont pas séparables, c'est-à-
dire que, rigoureusement, on ne peut pas écrire la fonction
d'onde totale 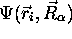 sous
la forme d'un produit de deux
fonctions d'onde séparées, l'une pour les noyaux, l'autre pour
les électrons.
sous
la forme d'un produit de deux
fonctions d'onde séparées, l'une pour les noyaux, l'autre pour
les électrons.
L'approximation de Born-Oppenheimer propose cependant une telle
forme de produit pour la fonction d'onde totale. Dans cette
approximation, on écrit
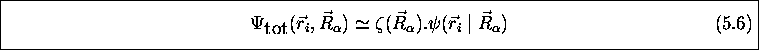
la fonction 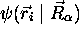 étant une fonction propre de
étant une fonction propre de 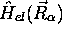 , (avec
valeur propre
, (avec
valeur propre 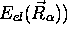 ; et de ce fait, elle dépend
paramétriquement de
; et de ce fait, elle dépend
paramétriquement de
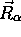 , tout comme elle dépend de la valeur de bien
d'autres
paramètres: la charge e, le numéro de charge
, tout comme elle dépend de la valeur de bien
d'autres
paramètres: la charge e, le numéro de charge 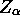 des noyaux, la
constante de Planck
des noyaux, la
constante de Planck 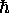 , etc. On souligne cependant cette
dépendance paramétrique de
, etc. On souligne cependant cette
dépendance paramétrique de 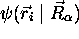 sur
sur 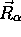 , car sa présence fait
que (5.6) ne représente pas une séparation de
variables authentique, comme on l'avait apprise auparavant. On
dit que (5.6) représente une séparation adiabatique
entre les électrons et les noyaux. Si l'on laisse agir
l'hamiltonien total
, car sa présence fait
que (5.6) ne représente pas une séparation de
variables authentique, comme on l'avait apprise auparavant. On
dit que (5.6) représente une séparation adiabatique
entre les électrons et les noyaux. Si l'on laisse agir
l'hamiltonien total 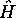 sur cette expression de
sur cette expression de 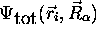 , alors
on obtient l'expression suivante de l'équation de Schrödinger
, alors
on obtient l'expression suivante de l'équation de Schrödinger
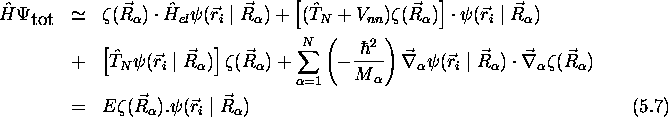
Si l'on considère que 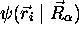 ne dépend que faiblement des
coordonnées nucléaires
ne dépend que faiblement des
coordonnées nucléaires 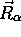 , alors les termes
, alors les termes
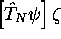 et
et 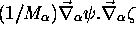 dans (5.7), termes
dits couplages non-adiabatiques, peuvent être négligés
vis-à-vis des termes restants; en particulier ces couplages
non-adiabatiques sont généralement bien plus faibles que le terme
dans (5.7), termes
dits couplages non-adiabatiques, peuvent être négligés
vis-à-vis des termes restants; en particulier ces couplages
non-adiabatiques sont généralement bien plus faibles que le terme
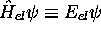 , dû au fait
que
, dû au fait
que  . Sans ces termes de couplage non-adiabatique,
(5.7) se réduit à
. Sans ces termes de couplage non-adiabatique,
(5.7) se réduit à
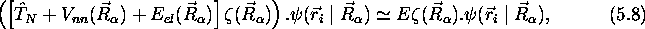
ou, simplement
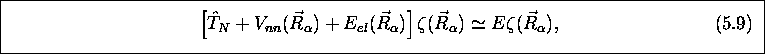
qui représente une équation aux valeurs propres pour 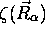 . Cette équation a la forme d'une équation de
Schrödinger pour le mouvement nucléaire, avec un potentiel effectif
. Cette équation a la forme d'une équation de
Schrödinger pour le mouvement nucléaire, avec un potentiel effectif
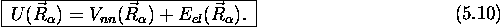
La fonction 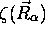 est appelée fonction d'onde
nucléaire; elle décrit les vibrations et les rotations de la
molécule dans un état électronique donné. En effet, pour
chaque état propre
est appelée fonction d'onde
nucléaire; elle décrit les vibrations et les rotations de la
molécule dans un état électronique donné. En effet, pour
chaque état propre 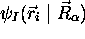 de
l'hamiltonien électronique,
de
l'hamiltonien électronique, 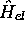 , le potentiel
gouvernant ces mouvements, (5.10), dépend de la
valeur propre associée
, le potentiel
gouvernant ces mouvements, (5.10), dépend de la
valeur propre associée 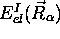 , et les
mouvements nucléaires, donc les états vibrationnels et rotationnels,
diffèrent d'un état électronique à un autre. On appelle les
différentes fonctions
, et les
mouvements nucléaires, donc les états vibrationnels et rotationnels,
diffèrent d'un état électronique à un autre. On appelle les
différentes fonctions 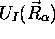 , définies par
(5.10), courbes ou surfaces d'énergie
potentielle.
, définies par
(5.10), courbes ou surfaces d'énergie
potentielle.
En résumé, dans l'approximation de Born-Oppenheimer, on écrit la
fonction d'onde totale sous la forme du produit d'une fonction
d'onde électronique avec une fonction d'onde nucléaire. La
fonction d'onde électronique dépend paramétriquement de la
géométrie nucléaire et est une fonction propre de l'hamiltonien
électronique. La somme de la valeur propre associée, (l'énergie
électronique), et du potentiel de répulsion coulombienne 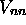 définit un potentiel effectif qui gouverne les mouvements
nucléaires. Ceux ci varient donc d'un état électronique à un
autre.
définit un potentiel effectif qui gouverne les mouvements
nucléaires. Ceux ci varient donc d'un état électronique à un
autre.




Next: Symétrie des orbitales:
Up: Approximation de Born-Oppenheimer
Previous: Hamiltonien moléculaire
Cours WWW Intro a la Chimie Quantique
Sat Jan 13 22:02:54 EST 2001
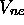 sur
sur 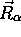 , l' hamiltonien
électronique
, l' hamiltonien
électronique 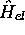 dépend
paramétriquement des coordonnées nucléaires. Il ne commute donc
pas avec l'opérateur
dépend
paramétriquement des coordonnées nucléaires. Il ne commute donc
pas avec l'opérateur 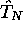 , et comme ces deux opérateurs
apparaissent dans l'hamiltonien moléculaire
, et comme ces deux opérateurs
apparaissent dans l'hamiltonien moléculaire 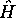 , les mouvements
électroniques et nucléaires ne sont pas séparables, c'est-à-
dire que, rigoureusement, on ne peut pas écrire la fonction
d'onde totale
, les mouvements
électroniques et nucléaires ne sont pas séparables, c'est-à-
dire que, rigoureusement, on ne peut pas écrire la fonction
d'onde totale 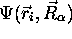 sous
la forme d'un produit de deux
fonctions d'onde séparées, l'une pour les noyaux, l'autre pour
les électrons.
sous
la forme d'un produit de deux
fonctions d'onde séparées, l'une pour les noyaux, l'autre pour
les électrons.
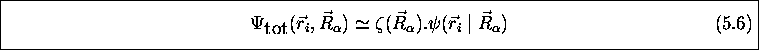
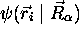 étant une fonction propre de
étant une fonction propre de 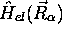 , (avec
valeur propre
, (avec
valeur propre 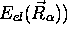 ; et de ce fait, elle dépend
paramétriquement de
; et de ce fait, elle dépend
paramétriquement de
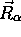 , tout comme elle dépend de la valeur de bien
d'autres
paramètres: la charge e, le numéro de charge
, tout comme elle dépend de la valeur de bien
d'autres
paramètres: la charge e, le numéro de charge 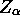 des noyaux, la
constante de Planck
des noyaux, la
constante de Planck 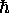 , etc. On souligne cependant cette
dépendance paramétrique de
, etc. On souligne cependant cette
dépendance paramétrique de 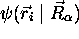 sur
sur 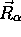 , car sa présence fait
que (
, car sa présence fait
que (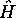 sur cette expression de
sur cette expression de 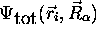 , alors
on obtient l'expression suivante de l'équation de Schrödinger
, alors
on obtient l'expression suivante de l'équation de Schrödinger
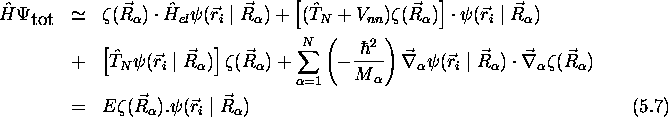
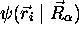 ne dépend que faiblement des
coordonnées nucléaires
ne dépend que faiblement des
coordonnées nucléaires 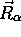 , alors les termes
, alors les termes
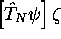 et
et 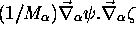 dans (
dans (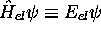 , dû au fait
que
, dû au fait
que  . Sans ces termes de couplage non-adiabatique,
(
. Sans ces termes de couplage non-adiabatique,
(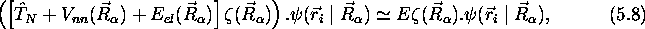
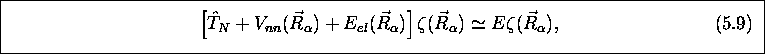
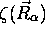 . Cette équation a la forme d'une équation de
Schrödinger pour le mouvement nucléaire, avec un potentiel effectif
. Cette équation a la forme d'une équation de
Schrödinger pour le mouvement nucléaire, avec un potentiel effectif
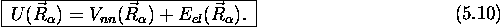
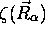 est appelée fonction d'onde
nucléaire; elle décrit les vibrations et les rotations de la
molécule dans un état électronique donné. En effet, pour
chaque état propre
est appelée fonction d'onde
nucléaire; elle décrit les vibrations et les rotations de la
molécule dans un état électronique donné. En effet, pour
chaque état propre 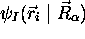 de
l'hamiltonien électronique,
de
l'hamiltonien électronique, 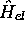 , le potentiel
gouvernant ces mouvements, (
, le potentiel
gouvernant ces mouvements, (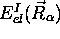 , et les
mouvements nucléaires, donc les états vibrationnels et rotationnels,
diffèrent d'un état électronique à un autre. On appelle les
différentes fonctions
, et les
mouvements nucléaires, donc les états vibrationnels et rotationnels,
diffèrent d'un état électronique à un autre. On appelle les
différentes fonctions 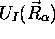 , définies par
(
, définies par
(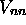 définit un potentiel effectif qui gouverne les mouvements
nucléaires. Ceux ci varient donc d'un état électronique à un
autre.
définit un potentiel effectif qui gouverne les mouvements
nucléaires. Ceux ci varient donc d'un état électronique à un
autre.