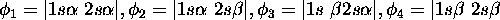
La configuration
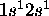donne lieu à 4 déterminants de Slater distincts:
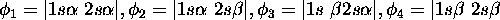
À l'ordre zéro, ces 4 déterminants ont la même énergie. Ils ont tous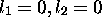 
et 
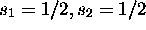. Selon la règle du triangle, on a donc
et
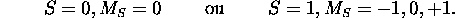
On peut donc avoir deux termes spectraux: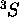 
et 
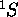. Le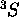 
comporte 3 états:
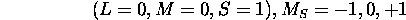
Il est clair que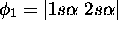 
est un état avec 
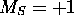. Il appartient nécessairement au 
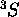. De même pour 
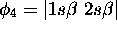qui est l'état avec 
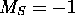du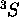 
. Il reste 
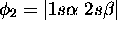et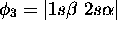 
, qui sont tous des états propres de 
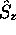avec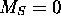 
. Ni l'un, ni l'autre n'est cependant un état propre de 
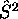, mais les combinaisons linéaires 
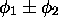le sont. En fait, on montre que:
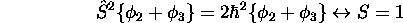
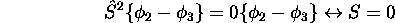
En résumé, la configuration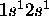 
comporte 4 états, que l'on peut regrouper en 2 termes spectraux, un 
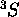(comportant 3 états, 
, 
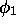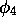et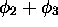 
) et un 
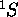(comportant un seul état, 
).
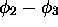Dans cette configuration à 2 électrons, S=0,1 toujours comme dans l'exemple précédent. En plus, avec
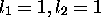, on peut avoir L=0,1. Sans encore tenir compte du principe de Pauli, on prévoit donc les termes suivants:
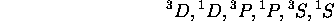
Ce qui donnerait un total de 36 états. Or, en considérant tous les déterminants de Slater que l'on peut écrire à partir de la configuration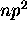 
, on ne trouve que 15 états. Il est clair que certains des termes énumérés ne sont pas permis, à cause du principe de Pauli. On peut trouver les termes associés à cette configuration en procédant par élimination comme suit:
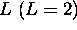et le plus grand 
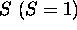, soit le 
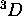. Si ce terme existe, on doit pouvoir construire un déterminant de Slater avec M=+2 et 
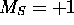. Le seul déterminant que l'on peut envisager de ce type est 
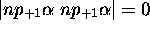: Le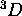 
est interdit par le principe de Pauli.
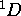, doit donner lieu à un état avec M=+2 (donc 
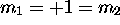nécessairement) et 
(
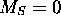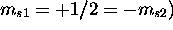. Le déterminant 
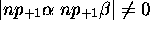correspond bien à cette description. Le terme 
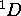existe,
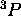. S'il existe, on devrait pouvoir trouver un état avec 
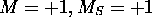. On peut en effet construire le déterminant 
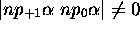qui correspond bien à cette description. Par conséquent, le terme 
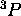existe.
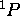existe, on doit trouver, non pas un seul état avec M=+1 et 
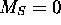, car un tel état doit forcément exister, vu les termes 
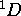et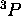 
que l'on a établis auparavant. Comme chacun de ces deux termes contient un état avec 
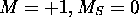, on doit pouvoir construire jusqu'à trois états de ce type pour établir l'existence du 
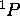. Or, on n'en trouve que deux réalisations possibles:
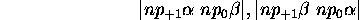
Le terme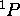 
n'existe donc pas.
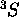: s'il existe, on doit pouvoir trouver deux états avec 
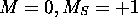. Seul le déterminant
est trouvé (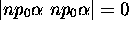
est interdit). Il doit nécessairement faire partie du 
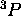déjà établi. Le terme 
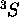n'existe donc pas.
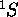existe, car on trouve trois états avec 
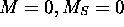(deux appartiennent aux deux termes déjà établis): 
, 
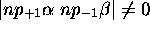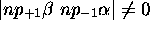et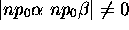 
.
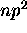ne peut donner lieu qu'aux trois termes suivants:
Remarques:
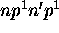tous les termes
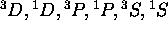sont permis.
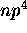donne lieu aux mêmes termes que la configuration 
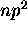. En général, la configuration 
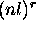donne lieu aux mêmes termes que la configuration 
.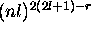