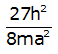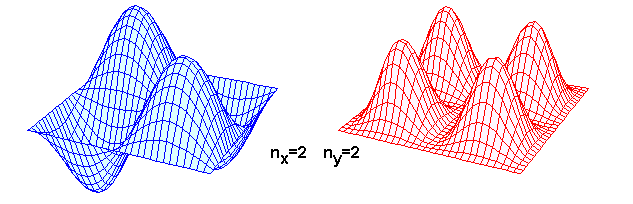
On peut modéliser une porphyrine typique comme 26 électrons confinés dans une boite carrée de 1 nm de coté.
- Représenter schématiquement tous les niveaux d'énergie permis entre 0 et
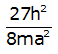
- Placer les 26 électrons sur ces niveaux, sachant que chaque fonction d'onde ne peut décrire les propriétés de plus de 2 électrons.
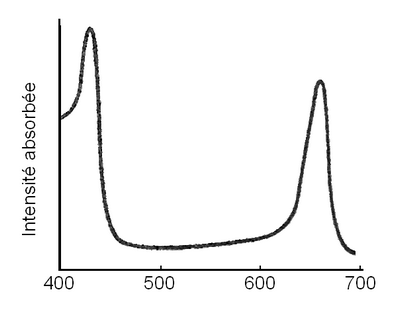
- Le spectre d'absorption de la molécule est reproduit ci-contre. La longueur d'onde la plus grande sur le spectre est λmax=660 nm. Calculer la valeur de λmax prédite par le modèle.
λmax = 659 nm
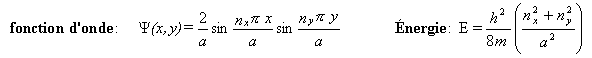
 On peut modéliser une porphyrine typique comme 26 électrons confinés dans une boite carrée de 1 nm de coté.
On peut modéliser une porphyrine typique comme 26 électrons confinés dans une boite carrée de 1 nm de coté.