Ce système est décrit par le potentiel suivant
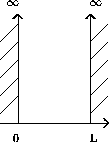
Figure 2.1: Potentiel d'une particule dans une boîte unidimensionnelle
Comme l'illustre la figure 2.1, ce potentiel comporte un mur
impénétrable en x = 0 et x = L. À cause de ce mur de potentiel
infiniment haut, la particule ne peut pas se trouver à
l'extérieur de l'intervalle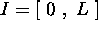 
. Sa fonction d'onde doit
nécessairement s'annuler dès que x atteint les bornes de
l'intervalle.
Par conséquent, on ne doit résoudre l'équation de Schrödinger
que pour 
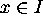, c.à.d. l'équation
avec conditions aux bornes
L'équation différentielle (2.1) admet comme solution générale
avec
L'imposition de la première condition aux bornes,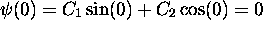
implique 
,
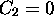et (2.3) se réduit à
La seconde condition aux bornes, se lit alors
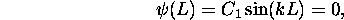
ce qui implique que le produit k L est un multiple entier de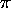 
, ou
On a joint l'index n à k pour spécifier que cette quantité
(un nombre d'onde) dépend du nombre quantique n. Notons que
seules des valeurs entières positives de n sont à retenir, car en
changeant le signe de n, on ne fait que changer la phase de la
fonction d'onde. On note aussi que la valeur n = 0 a été exclue
car elle donnerait une solution inacceptable, la solution
triviale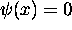 
, 
.
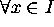Rappelant la relation entre k et l'énergie E, (2.4), on obtient de (2.5) une loi de quantification de l'énergie
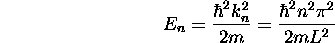
ou encore
On voit clairement dans ce cas, que la quantification de l'énergie découle de l'imposition des conditions aux bornes (2.2) ou encore du caractère de la fonction d'onde qui doit être de carré sommable.
On a trouvé dans les paragraphes précédents que les fonctions propres de
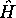associées aux valeurs propres 
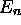de
(2.6), sont de la forme
où n est un entier non nul. La constante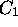 
dans cette
expression est déterminée par normalisation, c.à.d. par la
condition
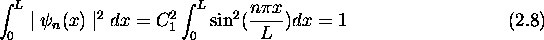
On trouve alors
,
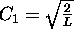et l'expression finale de la fonction d'onde associée à la valeur
propre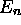 
se lit donc
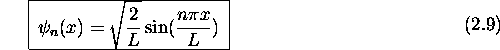
On peut déduire de cette expression les propriétés principales suivantes des fonctions d'onde décrivant les états stationnaires de la particule dans une boite:
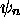et des
densités de probabilité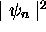 
pour les quelques
premiers niveaux d'énergie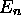 
. On remarque que, en plus des
points x = 0 et x = L,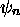 
a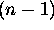 
zéros situés en
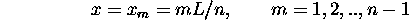
Ces points, où la fonction d'onde et la densité de probabilité
sont nulles, sont appellés points nodaux ou simplement
noeuds de la fonction d'onde. Le nombre de noeuds augmente
quand n augmente, c.à.d quand l'on passe à des états de plus
en plus excités. La fonction d'onde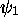 
de l'état
fondamental (situé à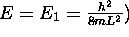 
n'a
pas de noeuds, celle du premier état excité,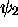 
,
d'énergie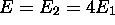 
, a un point nodal, celle du deuxième
état excité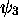 
a deux points nodaux, etc... La variation
des propriétés nodales des fonctions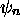 
quand n varie
traduit l'orthogonalité des états stationnaires d'énergie
différente. En effet, on vérifie aisément que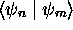 
est nul quand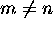 
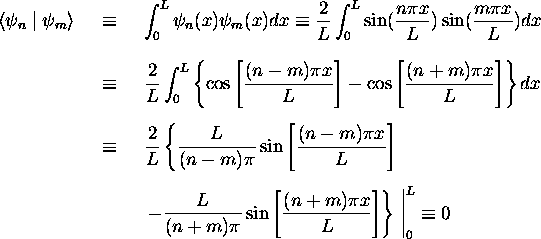
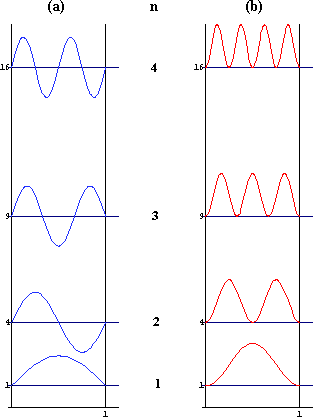
Figure 2.2: (a)Fonction d'onde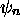 
et (b)densité de
probabilité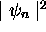 
, n = 1,2,3,4, pour une particule dans une
boîte unidimensionnelle
Comme on peut le voir sur la figure 2.2, la densité de
probabilité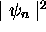 
associée à tout état stationnaire
de la particule est symmétrique par rapport au point médian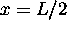 
.
On anticipe donc que la valeur moyenne de x sera exactement égale
à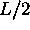 
dans un tel état. En effet
ce qui donne finalement
On vérifie aisément aussi que la valeur moyenne d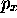e 
, la
quantité de mouvement le long de x, est nulle dans tout état
stationnaire, c.à.d. que
