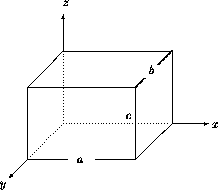
Figure 2.3: Boîte tri-dimensionelle
On considère maintenant une particule se mouvant librement dans la boîte tridimensionnelle de la figure 2.3.

Figure 2.3: Boîte tri-dimensionelle
L'énergie potentielle de ce système est donnée par
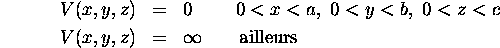
Comme dans le cas unidimensionnelle, les murs de potentiel infini
empêchent la particule de quitter la boîte, et la fonction d'onde
n'est non nulle que pour 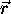 se trouvant à l'intérieur de la
boite. Elle s'annulle nécessairement dès que l'un des murs est
atteint. L'équation de Schrödinger que l'on doit résoudre est
donc
se trouvant à l'intérieur de la
boite. Elle s'annulle nécessairement dès que l'un des murs est
atteint. L'équation de Schrödinger que l'on doit résoudre est
donc
et les conditions aux bornes se lisent
Notons que l'hamiltonien du système est de la forme
où
Une telle forme est dite séparable: l'hamiltonien est une somme
d'opérateurs individuels 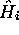 , chacun ne dépendant que d'une
seule variable ou degré de liberté
, chacun ne dépendant que d'une
seule variable ou degré de liberté 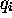 . Cette forme traduit le
caractère indépendant des mouvements décrits par les variables
. Cette forme traduit le
caractère indépendant des mouvements décrits par les variables
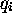 . Rappelons-nous que la probabilité conjointe de deux
évènements indépendants est le produit des probabilités
individuelles des deux évènements, pris séparément. On s'attend
donc à ce que la densité de probabilité de présence dans l'espace
de configuration multidimensionnel soit, dans le cas où
l'hamiltonien est de forme séparable, un simple produit de
densités de probabilité individuelles. En fait, la forme
séparable de l'hamiltonien permet une séparation de variables sur
la fonction d'onde elle-même.
. Rappelons-nous que la probabilité conjointe de deux
évènements indépendants est le produit des probabilités
individuelles des deux évènements, pris séparément. On s'attend
donc à ce que la densité de probabilité de présence dans l'espace
de configuration multidimensionnel soit, dans le cas où
l'hamiltonien est de forme séparable, un simple produit de
densités de probabilité individuelles. En fait, la forme
séparable de l'hamiltonien permet une séparation de variables sur
la fonction d'onde elle-même.
Séparation de variables
Écrivons les solutions de (2.12) sous la forme
d'un produit de trois facteurs: le premier, 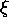 , ne dépend que de
x, le second,
, ne dépend que de
x, le second, 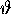 , ne dépend que de y, et le dernier
facteur
, ne dépend que de y, et le dernier
facteur 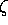 est une fonction de z seulement.
est une fonction de z seulement.
Substituant (2.20) dans (2.12), on obtient
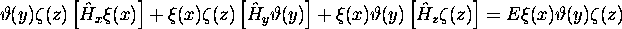
ou encore, en divisant les deux membres de ceci par 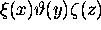 :
:
Cette équation demande que la somme des trois termes dans le membre de gauche soit égale à une constante. Chacun de ces trois termes ne dépendant que d'une et une seule variable, pour que leur somme soit égale à une constante, il faut que chaque terme soit lui même constant. En effet, en prenant la dérivée des deux membres de (2.21) par rapport à x, par exemple, on a
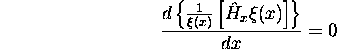
ce qui signifie que 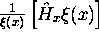 doit être égale à une constante; appellons-la
doit être égale à une constante; appellons-la 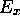 ,
on a alors
,
on a alors
De même, on obtient
et
où 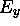 et
et 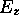 sont des constantes.
sont des constantes.
Notons que chacune des équations séparées que l'on vient
d'obtenir, pour le mouvement de la particule dans les trois
directions x,y et z, est l'équation de Schrödinger dans une boite
unidimensionelle. Ainsi, (2.22) décrit le mouvement
dans la direction des x, limité à l'intervalle 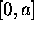 ; elle doit
être résolue avec conditions aux bornes
; elle doit
être résolue avec conditions aux bornes
De même, (2.23) décrit le mouvement dans la direction
des y limité à l'intervalle 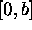 et doit être résolue avec
conditions aux bornes
et doit être résolue avec
conditions aux bornes
Finalement, (2.24) décrit le mouvement en z restreint à
l'intervalle 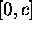 . Elle exige les conditions aux bornes
. Elle exige les conditions aux bornes
Les résultats de la section précédente peuvent donc être utilisés directement, et donnent
En résumé les états stationnaires de la particule dans la boite
tridimensionnelle sont spécifiés par trois nombres quantiques
entiers strictement positifs, 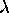 ,
, 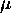 et
et  : Les fonctions
d'onde sont
: Les fonctions
d'onde sont
et leurs énergies sont
La technique de séparation de variables détaillée ci-haut, partant
de (2.20) pour aboutir à (2.31) et
(2.32), n'est applicable que parce que l'hamiltonien est
de forme séparable. On vérifie aisément, en utilisant
(2.31), que la densité de probabilité tridimensionnelle
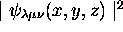 est le produit des
densités de probabilité unidimensionnelles,
est le produit des
densités de probabilité unidimensionnelles, 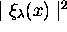 ,
, 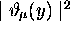 et
et 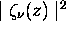 , comme on l'avait anticipé. On note aussi que l'énergie
de mouvement dans l'espace tridimensionnel est la somme des énergies de
mouvement dans les trois directions x, y et z: l'indépendance de
ces trois directions, ou degrés de liberté, implique donc
l'additivité de leur énergie.
, comme on l'avait anticipé. On note aussi que l'énergie
de mouvement dans l'espace tridimensionnel est la somme des énergies de
mouvement dans les trois directions x, y et z: l'indépendance de
ces trois directions, ou degrés de liberté, implique donc
l'additivité de leur énergie.
On note que, dans le cas où la boîte est un parallélépipède irrégulier, c'est-à-dire que
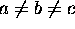 , le potentiel est
complètement asymmétrique, et tous les niveaux sont non-dégénérés:
à chaque niveau
, le potentiel est
complètement asymmétrique, et tous les niveaux sont non-dégénérés:
à chaque niveau 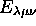 , ne correspond qu'un seul état, décrit par
, ne correspond qu'un seul état, décrit par
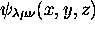 . Par contre, dans le cas où le
potentiel possède une
symmétrie, traduite par l'égalité d'au moins deux côtés de la
boîte, certains niveaux sont dégénérés. Par exemple, dans le cas
d'une boîte cubique, a = b = c, chaque niveau
. Par contre, dans le cas où le
potentiel possède une
symmétrie, traduite par l'égalité d'au moins deux côtés de la
boîte, certains niveaux sont dégénérés. Par exemple, dans le cas
d'une boîte cubique, a = b = c, chaque niveau 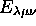 avec
avec
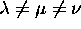 est sextuplement dégénéré, les six états qui y sont associés étant
est sextuplement dégénéré, les six états qui y sont associés étant
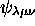 ,
, 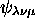 ,
, 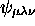 ,
, 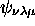 ,
, 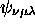 et
et
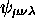 (ils sont obtenus en
considérant toutes les permutations possibles de
(ils sont obtenus en
considérant toutes les permutations possibles de 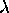 ,
, 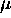 ,
,
 ). De même, un niveau
). De même, un niveau 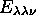 , où deux des
nombres quantiques
, où deux des
nombres quantiques 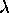 ,
, 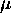 ,
,  sont
égaux, est triplement dégénéré, les trois états associés
étant
sont
égaux, est triplement dégénéré, les trois états associés
étant
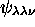 ,
, 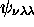 et
et 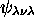 . Ainsi, les deux premiers niveaux d'une
particule dans un boîte cubique sont
. Ainsi, les deux premiers niveaux d'une
particule dans un boîte cubique sont
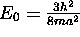 ,
non dégénéré, le seul état y étant associé est
,
non dégénéré, le seul état y étant associé est 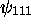 .
.
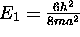 , triplement dégénéré, les trois états y étant
associés sont
, triplement dégénéré, les trois états y étant
associés sont 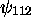 ,
, 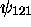 et
et 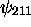 .
.
Partant d'une boîte symmétrique, par exemple la boîte cubique que l'on vient de considérer, une levée de dégénérescence des niveaux est obtenue en déformant la boîte, car une telle déformation réduit la symmétrie du système. On distingue deux cas:
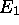 du cas cubique se scinde en deux niveaux:
du cas cubique se scinde en deux niveaux:
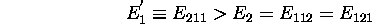
Le niveau 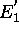 est non-dégénéré, mais le niveau
est non-dégénéré, mais le niveau 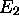 demeure dégénéré: deux états y sont associés, les états
demeure dégénéré: deux états y sont associés, les états
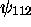 et
et 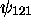 .
.
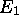 du cas cubique se scinde en trois niveaux
non-dégénérés:
du cas cubique se scinde en trois niveaux
non-dégénérés:
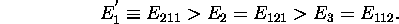
La discussion précédente sert à illustrer la relation entre la symmétrie du système et la dégénérescence des niveaux: Un degré de symmétrie élevé favorise plus l'apparition de niveaux dégénérés qu'un faible degré de symmétrie.