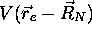 . On ne peut
donc pas
effectuer une séparation de variables entre
. On ne peut
donc pas
effectuer une séparation de variables entre 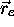 et
et 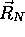 . Par
contre, une
séparation de variables est possible entre la coordonnée du centre de
masse
. Par
contre, une
séparation de variables est possible entre la coordonnée du centre de
masse
Les mouvements des deux particules sont corrélés car les deux charges
interagissent à travers le potentiel 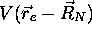 . On ne peut
donc pas
effectuer une séparation de variables entre
. On ne peut
donc pas
effectuer une séparation de variables entre 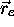 et
et 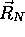 . Par
contre, une
séparation de variables est possible entre la coordonnée du centre de
masse
. Par
contre, une
séparation de variables est possible entre la coordonnée du centre de
masse
et la coordonnée relative de l'électron par rapport au noyau
La disposition de ces nouveaux vecteurs de position, définis dans le système du centre de masse, par rapport aux anciens vecteurs de position, définis dans le système du laboratoire, est illustrée à la figure 3.1.
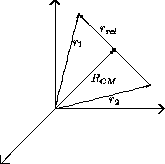
Figure 3.1: Référentiel du centre de masse
En utilisant les relations (3.3) et (3.4), et les lois de transformations correspondantes des impulsions, qui sont données par
on obtient, à partir de (3.1),
où
est la masse totale du système, et
est sa masse réduite.