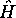On voit clairement que, dans le référentiel du centre de masse,
l'hamiltonien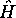 
est mis sous une forme séparable, car
(3.7) peut s'écrire
avec
et
En termes des coordonnées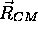 
et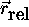 
,
la fonction d'onde
décrivant un état stationaire du système à deux corps est donc
un produit de fonctions d'onde individuelles, l'une pour le
mouvement du centre de masse, l'autre pour le mouvement relatif
et l'énergie de cet état est la somme des énergies de mouvement respectives.
avec
et
L'hamiltonien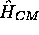 
apparaissant dans (3.15) a
été
défini plus haut; (3.11) décrit le mouvement du
centre de masse, ou le mouvement translationnel d'ensemble de
l'atome. Ce mouvement est celui d'une particule de masse 
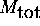dans une boite tridimensionnelle de volume infini. Les fonctions
propres et valeurs propres pour ce mouvement étant déjà obtenues
au chapitre précédent, on se limitera à l'étude de l'équation
séparée pour le mouvement relatif, ou mouvement interne,
(3.16). Comme aucune confusion ne serait plus
possible, à partir de la section suivante, nous laisserons
tomber, pour simplifier les notations, la mention rel en indice
inférieur.
