
On note que
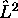 est un opérateur différentiel par rapport aux
angles
est un opérateur différentiel par rapport aux
angles 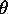 et
et 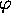 seulement. Il commute donc avec tout opérateur ne
dépendant que de la variable radiale r, dont l'opérateur
seulement. Il commute donc avec tout opérateur ne
dépendant que de la variable radiale r, dont l'opérateur 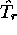 et le
potentiel
et le
potentiel 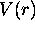 dans l'expression de
dans l'expression de 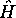 , (3.21).
C'était aussi ce fait qui nous a permis d'écrire le terme central
dans cette expression, le terme contenant le produit de
l'opérateur
, (3.21).
C'était aussi ce fait qui nous a permis d'écrire le terme central
dans cette expression, le terme contenant le produit de
l'opérateur 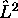 avec l'opérateur
avec l'opérateur 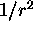 , sans prêter une
attention
particulière à l'ordre d'apparition de ces deux opérateurs. Par
conséquent,
, sans prêter une
attention
particulière à l'ordre d'apparition de ces deux opérateurs. Par
conséquent, 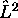 commute avec H. On a déjà vu que
commute avec H. On a déjà vu que 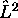 commute avec
n'importe quelle composante
commute avec
n'importe quelle composante 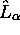 du vecteur moment cinétique. En
coordonnées polaires, la composante
du vecteur moment cinétique. En
coordonnées polaires, la composante 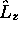 prend la forme
particulièrement simple suivante:
prend la forme
particulièrement simple suivante:
On vérifie alors que 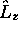 commute aussi avec
commute aussi avec 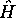 , étant un
opérateur
différentiel par rapport à l'angle
, étant un
opérateur
différentiel par rapport à l'angle 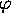 seulement.
seulement.
En résumé, on a
Le système admet donc deux constantes du mouvement, ( à part
l'énergie ): 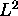 ou encore la longueur du vecteur moment cinétique
ou encore la longueur du vecteur moment cinétique
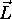 , et une de ses composantes, désignée ici arbitrairement comme
étant la composante
, et une de ses composantes, désignée ici arbitrairement comme
étant la composante 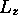 . Notons bien que seule une composante de
. Notons bien que seule une composante de 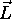 peut être spécifiée simultanément avec l'énergie E et la longueur
peut être spécifiée simultanément avec l'énergie E et la longueur
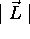 . Ceci découle du fait que les trois composantes de
. Ceci découle du fait que les trois composantes de
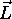 ne sont pas mutuellement commutatives.
ne sont pas mutuellement commutatives.