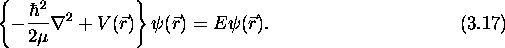
Avec
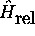 donné par (3.12), l'équation
de Schrödinger pour le mouvement relatif, (3.16), est
donné par (3.12), l'équation
de Schrödinger pour le mouvement relatif, (3.16), est
Dans le cas où le potentiel 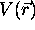 est centrosymétrique, c'est-
à-dire qu'il ne dépend que de la longueur du vecteur position
est centrosymétrique, c'est-
à-dire qu'il ne dépend que de la longueur du vecteur position 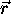 ,
et non de son orientation, l'équation (3.17), telle
qu'écrite, en coordonnées cartésiennes, n'est pas séparable; en
effet, en coordonnées cartésiennes, la longueur de
,
et non de son orientation, l'équation (3.17), telle
qu'écrite, en coordonnées cartésiennes, n'est pas séparable; en
effet, en coordonnées cartésiennes, la longueur de 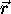 est
est
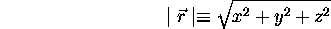
et le potentiel V n'est pas séparable en trois composantes chacune ne dépendant que d'une seule des trois variables x,y et z. L'hamiltonien n'est donc pas de forme séparable. Cependant, l'équation de Schrödinger (3.17) est séparable en coordonnées polaires définies par
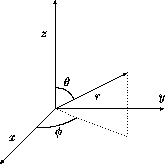
Figure 3.2: Définition des coordonnées polaires 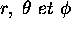
car, dans ce système de coordonnées, illustré à la figure
3.2, le potentiel ne dépend que d'une des trois
variables polaires, le rayon r. Il est indépendant des deux
angles 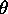 et
et 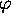 . On montre, après un long et fastidieux
développement mathématique, que l'hamiltonien
. On montre, après un long et fastidieux
développement mathématique, que l'hamiltonien 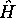 prend la forme
suivante en coordonnées polaires:
prend la forme
suivante en coordonnées polaires:
où
est l'opérateur énergie cinétique pour le mouvement radial de
l'électron par rapport au noyau, et 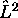 est l'opérateur associé au
carré du vecteur moment cinétique (voir chapitre 1).
En coordonnées polaires, cet opérateur s'écrit
est l'opérateur associé au
carré du vecteur moment cinétique (voir chapitre 1).
En coordonnées polaires, cet opérateur s'écrit
Dans ce cas, r est fixé, correspondant à

L'hamiltonien se réduit alors à