Quantification d'un moment angulaire

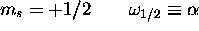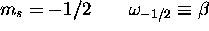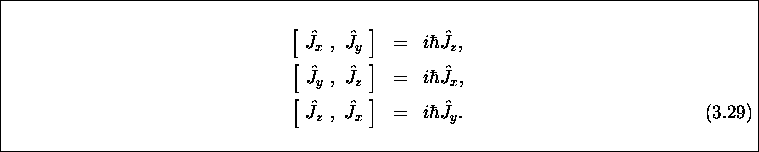
Le moment cinétique 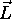est un exemple de moment angulaire. Un moment angulaire est un triplet d'opérateurs 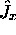, 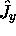et 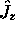satisfaisant aux relations de commutation suivantes, dites relations de commutation cycliques:

On peut montrer, de façon tout à fait générale, que

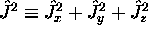1. l'opérateur commute avec n'importe quelle composante 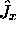, 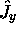ou

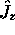
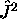2. les vecteurs propres communs de et de 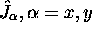ou z, (on prend généralement 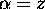), sont spécifiés par deux nombres quantiques j et 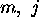pouvant être entier ou demi-entier, mais est toujours positif, et m varie par pas entier de -j jusqu'à +j.

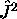3. les valeurs propres de sont gouvernées par j

    

   tandis que celles de 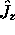sont gouvernées par m

    

Il est important de noter que ces résultats découlent strictement et rigoureusement des relations de commutation cycliques 3.29, c'est-à-dire qu'elle peuvent se démontrer de façon purement algébrique.

Moment cinétique

Dans le cas du moment cinétique 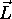, dont les composantes sont des opérateurs différentielles par rapport aux angles 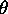et 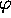, et dont les fonctions propres 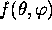doivent satisfaire à une condition de périodicité du type

on montre que le nombre quantique m doit être entier (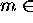 Z), et le nombre quantique j, appelé communément l plutôt, est nécessairement entier. Les fonctions propres communes à 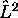et 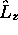sont appelées harmoniques sphériques; on les note 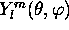. Elles sont de la forme générale suivante:

où 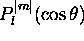est une fonction spéciale de 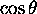connue en mathématique sous le nom de 'fonction associée de Legendre'. On trouve au tableau 3.1 l'expression explicite de cette fonction pour les premières valeurs de l. Le tableau 3.2 donne l'expression des premières harmoniques sphériques .

  
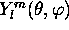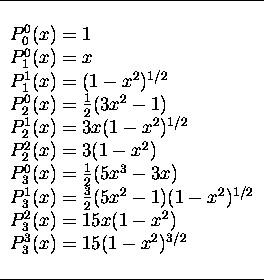
Table: Les premières fonctions associées de Legendre. Dans toutes les expressions montrées

  
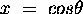
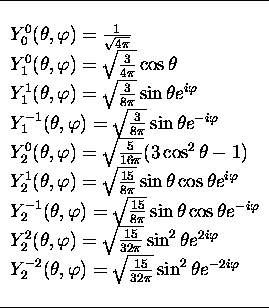
Table 3.2: Expression explicite des premières harmoniques sphériques

Spin

Il existe des moments angulaires qui, contrairement à 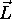, le moment cinétique orbital, n'ont pas d'équivalent classique. Le spin en est un exemple. Dans ce cas, aucune contrainte due à une condition de périodicité normale n'est nécessaire, et on peut avoir j demi-entier. Chaque particule a un spin avec un nombre quantique j fixé, que l'on désigne par s plutôt. L'électron, par exemple, a un spin 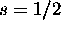. 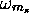Il ne peut donc être que dans l'un ou l'autre des deux états de spin, , suivants (il n'est pas nécessaire de mentionner le nombre quantique s dans l'état de spin, ce nombre étant fixé):