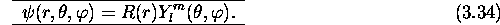
Les considérations des constantes de mouvements de la section précédente suggèrent que l'on écrive les fonctions propres de
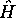 sous la forme suivante
sous la forme suivante
où 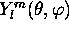 est une harmonique sphérique. Par définition,
c'est une fonction propre commune de
est une harmonique sphérique. Par définition,
c'est une fonction propre commune de 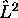 et
et 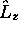 , avec valeur propre
, avec valeur propre 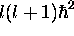 et
et 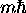 respectivement:
respectivement:
Dans ce cas, comme r est fixé à
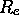 , et l'hamiltonien ne dépend que des angles
, et l'hamiltonien ne dépend que des angles 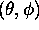 , le facteur
, le facteur 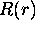 est une simple constante. En d'autres termes, les harmoniques sphériques
est une simple constante. En d'autres termes, les harmoniques sphériques 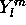 sont directement fonctions propres de
sont directement fonctions propres de 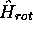 avec valeurs propres
avec valeurs propres 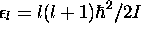
On montre, à partir des propriétés des harmoniques sphériques, que le spectre rotationnel pur est régi par la règle de sélection

Substituant (3.34) dans l'équation de Schrödinger, (3.17), avec l'hamiltonien
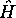 exprimé en coordonnées
polaires selon (3.21), on obtient une équation pour
le facteur radial
exprimé en coordonnées
polaires selon (3.21), on obtient une équation pour
le facteur radial 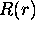 :
:
Dans le cas où 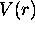 est le potentiel de Coulomb,
(3.2), cette équation radiale ne donne
lieu à une solution
est le potentiel de Coulomb,
(3.2), cette équation radiale ne donne
lieu à une solution 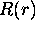 normable, c.à.d. qui ne diverge pas
ni à l'origine ni à l'infini, que pour des valeurs de
l'énergie répondant à la loi de quantification suivante
normable, c.à.d. qui ne diverge pas
ni à l'origine ni à l'infini, que pour des valeurs de
l'énergie répondant à la loi de quantification suivante
Le nombre quantique n est appellé nombre quantique principal.
Pour une valeur donnée de ce nombre, il existe plusieurs
solutions pour la fonction 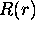 selon la valeur du nombre
quantique l. D'où l'identification des solutions de
(3.38) par la paire
selon la valeur du nombre
quantique l. D'où l'identification des solutions de
(3.38) par la paire 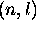 ; on les note
; on les note 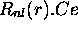 sont des fonctions réelles de la variable r; Elles possèdent
toutes la structure générale d'un produit d'une exponentielle
décroissante par un polynôme de degré n-l. Les premières
fonctions
sont des fonctions réelles de la variable r; Elles possèdent
toutes la structure générale d'un produit d'une exponentielle
décroissante par un polynôme de degré n-l. Les premières
fonctions 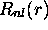 sont données au tableau 3.3. Leur
expression contient un paramètre constant qui a la dimension
d'une longueur:
sont données au tableau 3.3. Leur
expression contient un paramètre constant qui a la dimension
d'une longueur:
Cette constante est appellée rayon de Bohr et vaut 0.5292 Å .
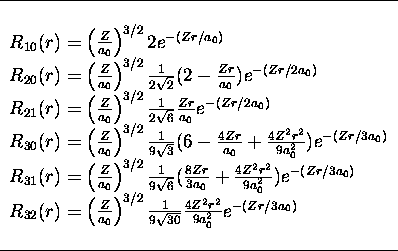
Table 3.3: Premières fonctions d'onde radiales de l'atome
hydrogénoïde
On trouve aussi que le nombre quantique l est soumis à la condition

ce nombre quantique est appellé nombre quantique azimutal. Le nombre quantique m, qui varie, rappelons-le, de -l à +l par valeurs entières, porte le nom de nombre quantique magnétique.