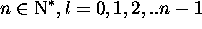 et
et 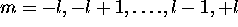 . Ces états sont décrits par
. Ces états sont décrits par
En résumé, les états stationaires de l'atome hydrogénoïde sont
spécifiés par trois nombres quantiques 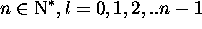 et
et 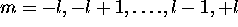 . Ces états sont décrits par
. Ces états sont décrits par
avec
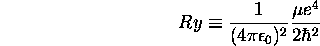
définissant la constante de Rydberg.
Les fonctions 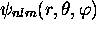 sont fonctions propres de
sont fonctions propres de
À chaque niveau 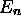 , correspond
, correspond 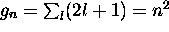 états
différents, distingués par la valeur de l et de m.
états
différents, distingués par la valeur de l et de m.
Les fonctions 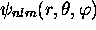 sont appellées
orbitales de l'atome. On
adopte la convention de nomenclature suivante de ces orbitales
(notation spectroscopique): chaque orbitale est caractérisée par
la valeur du nombre quantique n accompagnée par une lettre
minuscule reliée à la valeur du nombre quantique azimutal l. La
valeur du nombre quantique m est finalement spécifiée en indice.
On a ainsi:
sont appellées
orbitales de l'atome. On
adopte la convention de nomenclature suivante de ces orbitales
(notation spectroscopique): chaque orbitale est caractérisée par
la valeur du nombre quantique n accompagnée par une lettre
minuscule reliée à la valeur du nombre quantique azimutal l. La
valeur du nombre quantique m est finalement spécifiée en indice.
On a ainsi:
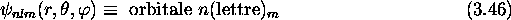
L'association d'une lettre à l'orbitale selon la valeur de l est définie au tableau 3.4.

Table 3.4: Convention de nomenclature des orbitales atomiques
Par exemple, l'état 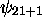 est appellé orbitale
est appellé orbitale 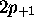 , l'état
, l'état 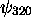 ,
l'orbitale
,
l'orbitale 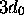 , etc. Sur le diagramme de la figure 3.3 on montre
explicitement les états distincts associés aux premiers niveaux
d'énergie de l'atome
, etc. Sur le diagramme de la figure 3.3 on montre
explicitement les états distincts associés aux premiers niveaux
d'énergie de l'atome 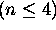 . La notation spectroscopique que
l'on vient de définir y était utilisée.
. La notation spectroscopique que
l'on vient de définir y était utilisée.
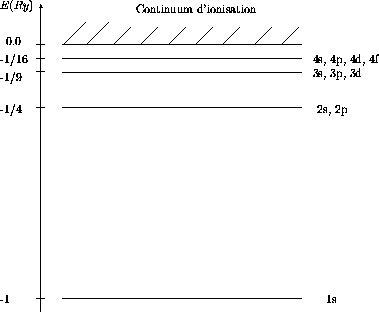
Figure 3.3: Premiers niveaux d'énergie de l'atome d'hydrogène.
Notons que toute orbitale 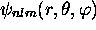 avec
avec 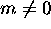 est complexe. Ce
caractère complexe provient de la partie angulaire
est complexe. Ce
caractère complexe provient de la partie angulaire 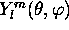 de
l'orbitale (voir (3.33)). Il est fréquent de remplacer
les fonctions complexes
de
l'orbitale (voir (3.33)). Il est fréquent de remplacer
les fonctions complexes 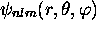 par des fonctions
réelles
obtenues en combinant linéairement
par des fonctions
réelles
obtenues en combinant linéairement 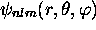 et
et
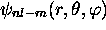 .
C'est ainsi que l'on obtient des orbitales réelles
.
C'est ainsi que l'on obtient des orbitales réelles 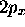 et
et 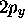 :
:
Ces fonctions continuent à être de bonnes fonctions propres de
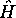 et de
et de 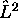 . Cependant elles ne sont plus des fonctions propres de
. Cependant elles ne sont plus des fonctions propres de
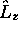 . L'avantage que présente leur utilisation réside dans le fait
qu'elles sont plus faciles à représenter graphiquement, et
aussi dans leur caractère directionnel plus évident. La dernière
ligne de (3.47) montre en effet que la fonction qui y
est définie se comporte comme la fonction x fois une fonction de
symétrie sphérique; d'où la notation
. L'avantage que présente leur utilisation réside dans le fait
qu'elles sont plus faciles à représenter graphiquement, et
aussi dans leur caractère directionnel plus évident. La dernière
ligne de (3.47) montre en effet que la fonction qui y
est définie se comporte comme la fonction x fois une fonction de
symétrie sphérique; d'où la notation 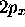 . De même, la fonction
de (3.48) se comporte comme le produit de y avec une
fonction de symétrie sphérique; d'où la notation
. De même, la fonction
de (3.48) se comporte comme le produit de y avec une
fonction de symétrie sphérique; d'où la notation 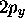 . Pour les
mêmes raisons, on appelle aussi la fonction
. Pour les
mêmes raisons, on appelle aussi la fonction 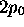 , orbitale
, orbitale 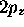 .
.
Spin-orbitales
On peut inclure le spin de l'électron dans la description de la structure électronique de l'atome. Si on traite le spin comme un degré de liberté additionnel --- degré de liberté qui n'a pas d'analogue classique --- alors, l'absence de terme d'interaction entre les degrés de liberté classiques (positions dans l'espace réelle) et le spin, interaction appelé couplage spin-orbite, dans l'hamiltonien tel que défini auparavent, (3.1), implique que l'on peut écrire la fonction d'onde totale, spin inclu, sous la forme de produit
Aux nombres quantiques n,l,m s'ajoute alors le nombre quantique
de spin 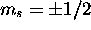 , et chaque niveau
, et chaque niveau 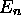 devient
devient 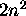 fois
dégénéré.
fois
dégénéré.
Les fonctions  sont appelées spin-orbitales: on
parle ainsi
de spin-orbitales
sont appelées spin-orbitales: on
parle ainsi
de spin-orbitales 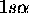 ,
, 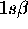 ,
, 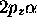 ,
, 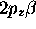 , etc. La notion
de spin-orbitale est surtout importante dans la discussion de la
structure électronique des systèmes à plusieurs électrons.
, etc. La notion
de spin-orbitale est surtout importante dans la discussion de la
structure électronique des systèmes à plusieurs électrons.