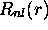 a
a 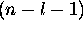 noeuds. Elle
contribue donc
noeuds. Elle
contribue donc 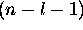 surfaces nodales sphériques à
l'orbitale
surfaces nodales sphériques à
l'orbitale 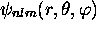 .
.
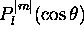 a
a 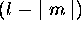 noeuds
noeuds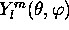 contribue donc
contribue donc 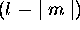 surfaces nodales coniques à l'orbitale
surfaces nodales coniques à l'orbitale
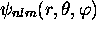 .
.
De l'expression générale des fonctions
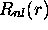 et
et 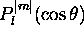 , on
trouve que
, on
trouve que
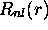 a
a 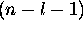 noeuds. Elle
contribue donc
noeuds. Elle
contribue donc 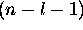 surfaces nodales sphériques à
l'orbitale
surfaces nodales sphériques à
l'orbitale 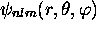 .
.
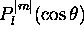 a
a 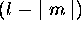 noeuds
noeuds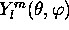 contribue donc
contribue donc 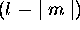 surfaces nodales coniques à l'orbitale
surfaces nodales coniques à l'orbitale
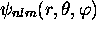 .
.
En tout, l'orbitale 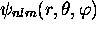 (de valeur complexe) a donc
(de valeur complexe) a donc
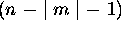 surfaces nodales.
surfaces nodales.
Considérons deux exemples:
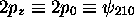 n'a qu'une seule surface
nodale, figure 3.4. C'est le plan xy, une surface
nodale conique contribuée par la fonction
n'a qu'une seule surface
nodale, figure 3.4. C'est le plan xy, une surface
nodale conique contribuée par la fonction 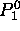 ; la fonction
; la fonction 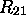 n'ayant aucun noeud.
n'ayant aucun noeud.
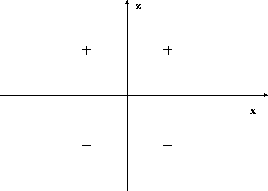
Figure 3.4: Propriété nodale de l'orbitale 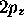
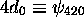 a trois surfaces nodales: une surface
nodale sphérique et deux surfaces nodales coniques. La
disposition de ces surfaces nodales est schématisée à la figure
3.5
a trois surfaces nodales: une surface
nodale sphérique et deux surfaces nodales coniques. La
disposition de ces surfaces nodales est schématisée à la figure
3.5
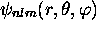 est bien réflété dans la représentation dite 'polaire' de sa partie angulaire
est bien réflété dans la représentation dite 'polaire' de sa partie angulaire 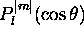 . La figure 3.6 illustre cette repésentation polaire pour un nombre d'orbitales.
. La figure 3.6 illustre cette repésentation polaire pour un nombre d'orbitales.

Figure: repésentation polaire de la partie angulaire pour une orbitale du type: a)np , b)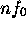 , c)
, c)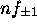 , d)
, d)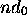 , e) orbitale
, e) orbitale
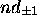 , f) orbitale
, f) orbitale
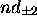
La partie radiale
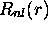 peut être visualisée directement sur un
graphique, comme illustré à la figure 3.7. Il est
cependant plus utile de considérer la quantité
peut être visualisée directement sur un
graphique, comme illustré à la figure 3.7. Il est
cependant plus utile de considérer la quantité 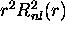 , car elle
représente une densité de probabilité de présence radiale, c'est-
à-dire que
, car elle
représente une densité de probabilité de présence radiale, c'est-
à-dire que 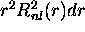 est la probabilité que l'électron se
trouve à une distance r du noyau, quel que soit l'orientation
de son vecteur de position; en effet, on vérifie facilement que
est la probabilité que l'électron se
trouve à une distance r du noyau, quel que soit l'orientation
de son vecteur de position; en effet, on vérifie facilement que
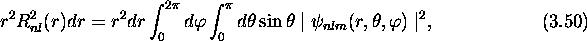
c'est-à-dire que 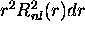 est la densité de probabilité de
présence tridimensionnelle
est la densité de probabilité de
présence tridimensionnelle 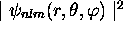 intégrée (sommée) sur
toutes les valeurs possibles des angles
intégrée (sommée) sur
toutes les valeurs possibles des angles 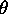 et
et 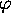 . La figure
3.7 montre aussi cette densité de probabilité radiale
pour un nombre de valeurs de n et l.
. La figure
3.7 montre aussi cette densité de probabilité radiale
pour un nombre de valeurs de n et l.
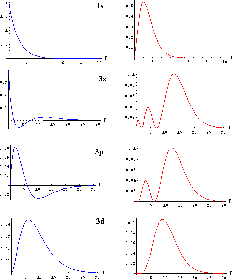
Figure: Représentation graphique de la fonction d'onde
radiale dans les orbitales 1s, 3s, 3p, 3d: À gauche, on trouve le graphes de la partie radiale 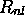 , et à droite, ceux de la distribution radiale
, et à droite, ceux de la distribution radiale 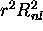 .
.
Il existe deux modes de représnetation graphique complète de la distribution de probabilité électronique:
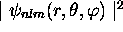 garde une
valeur constante
donnée. La figure 3.8 illustre ce procédé pour les orbitales
garde une
valeur constante
donnée. La figure 3.8 illustre ce procédé pour les orbitales 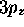 ,
, 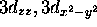 et
et
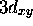 .
.
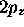 et
et 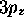 de l'atome d'hydrogène.
de l'atome d'hydrogène.
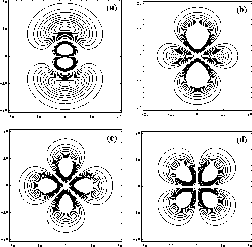
Figure 3.8: Courbes d'isodensité pour quelques orbitales de
l'atome d'hydrogène: a) orbitale 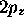 , b) orbitale
, b) orbitale
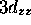 , c) orbitale
, c) orbitale 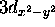 , d) orbitale
, d) orbitale
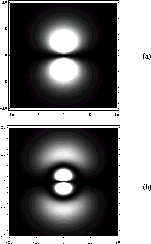
Figure: Cartes 'photographiques' de la densité totale dans: a) l'orbitale 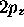 , b)l'orbitale
, b)l'orbitale
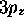 de
l'atome d'hydrogène.
de
l'atome d'hydrogène.