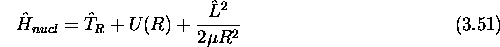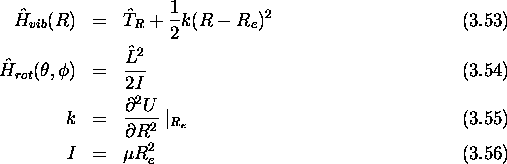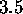 ), (
), (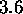 ) dans
(
) dans
(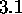 ), vérifiez le résultat donné en (
), vérifiez le résultat donné en (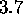 ).
).
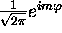 est
fonction propre de
est
fonction propre de 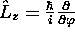 . Montrez qu'elle ne sastisfait à la condition
de périodicité (3.32) que si
. Montrez qu'elle ne sastisfait à la condition
de périodicité (3.32) que si 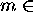 Z.
Z.
où 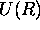 est le potentiel effectif dans un état électronique donné. Dans l'état fondamental des diatomiques stables,
est le potentiel effectif dans un état électronique donné. Dans l'état fondamental des diatomiques stables, 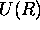 atteint un minimum à la distance internucléaire d'équilibre
atteint un minimum à la distance internucléaire d'équilibre 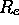 de la molécule. Il est alors d'usage de représenter
de la molécule. Il est alors d'usage de représenter 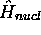 de eq.(3.51) sous la forme approchée:
de eq.(3.51) sous la forme approchée:
où
- Montrez que, sous cette forme approchée, l'hamiltonien
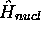 conduit à une équation de Schrödinger séparable.
conduit à une équation de Schrödinger séparable.
- En rappelant la loi de quantification de l'énergie d'un oscillateur harmonique et celle d'un moment cinétique, déduisez que l'énergie des mouvements nucléaires est quantifiée selon une loi de la forme suivante:
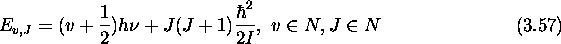
Quelle est la dégénérescence de chaque niveau
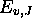 ?
?
- En admettant les règles de sélection
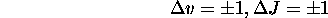
montrez que le spectre d'absorption ro-vibrationnelle de la molécule consiste en une bande avec deux branches, décrites par
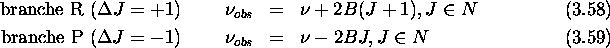
où
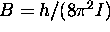 . Montrez que les raies dans chacune des branches R et P sont équidistantes. La position centrale de la bande est transparente (ne comporte pas de raie d'absorption). Expliquez ce fait.
. Montrez que les raies dans chacune des branches R et P sont équidistantes. La position centrale de la bande est transparente (ne comporte pas de raie d'absorption). Expliquez ce fait.
- Le spectre ro-vibrationnelle de
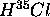 consiste en une bande centrée en
consiste en une bande centrée en 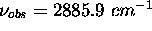 , avec des raies presque équidistantes, séparées par
, avec des raies presque équidistantes, séparées par 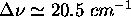 . À partir de
ces données, déterminez la constante de force k et la longueur de liaison d'équilibre,
. À partir de
ces données, déterminez la constante de force k et la longueur de liaison d'équilibre, 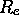 , pour cette molécule. Qu'arriverait-il au spectre si l'on fait la substitution isotopique
, pour cette molécule. Qu'arriverait-il au spectre si l'on fait la substitution isotopique 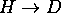 sur la molécule?
sur la molécule?
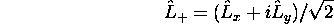
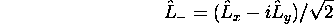
- Les opérateurs
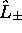 sont-ils hermitiques? Justifiez votre réponse.
sont-ils hermitiques? Justifiez votre réponse.
- Montrez que
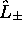 satisfont aux relations de commutation suivantes:
satisfont aux relations de commutation suivantes:


- Montrez que le produit
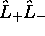 peut être exprimé sous la forme
peut être exprimé sous la forme
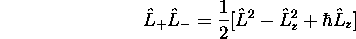
et qu'il est hermitique.
- Soit
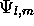 une fontion propre de
une fontion propre de 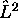 et de
et de 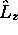 de nombres quantiques
de nombres quantiques 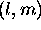 . En utilisant les relations de commutation précédentes, montrez que
. En utilisant les relations de commutation précédentes, montrez que 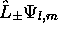 est aussi nécessairement fonction propre des mêmes opérateurs, et que les valeurs propres associées correspondent aux nombres quantiques
est aussi nécessairement fonction propre des mêmes opérateurs, et que les valeurs propres associées correspondent aux nombres quantiques 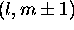 .
.
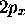 et
et 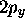 sont toujours des fonctions
propres de
sont toujours des fonctions
propres de 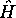 et
et 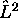 , mais ne sont pas fonctions
propres de
, mais ne sont pas fonctions
propres de 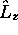 . Déterminez la probabilité de trouver a)
. Déterminez la probabilité de trouver a)
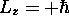 , b)
, b) 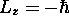 dans cet état. Quelle serait
la valeur moyenne de
dans cet état. Quelle serait
la valeur moyenne de 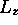 dans cet état?
dans cet état?
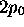 se comporte comme
se comporte comme 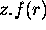 , où
, où 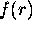 est
une fonction de la variable radiale r seulement.
est
une fonction de la variable radiale r seulement.
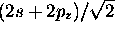 définit une
orbitale hybride sp. Montrez qu'elle est fonction propre de
définit une
orbitale hybride sp. Montrez qu'elle est fonction propre de 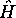 et de
et de 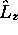 , mais pas de
, mais pas de 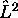 . Déterminez la
probabilité de trouver
. Déterminez la
probabilité de trouver 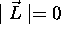 dans cet état.
dans cet état.
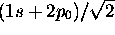 au temps t = 0.
Écrivez la fonction d'onde de l'atome à un temps t > 0.
Déterminez la probabilité de trouver l'atome au temps t avec a)
E = -Ry, b)
au temps t = 0.
Écrivez la fonction d'onde de l'atome à un temps t > 0.
Déterminez la probabilité de trouver l'atome au temps t avec a)
E = -Ry, b) 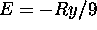 , c)
, c) 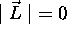 , d)
, d)
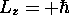 . Calculez la valeur moyenne de E,
. Calculez la valeur moyenne de E, 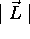 et
et 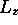 au temps t.
au temps t.
Dans les questions suivantes, on utiliserait la fonction de
distribution radiale 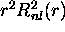 pour calculer les valeurs moyennes
de propriétés ne dépendant que de la variable radiale r. On aura
besoin de la formule suivante
pour calculer les valeurs moyennes
de propriétés ne dépendant que de la variable radiale r. On aura
besoin de la formule suivante
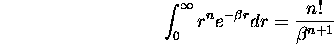
- Montrez que la valeur moyenne <r> vaut a)
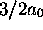 dans
l'état 1s, b)
dans
l'état 1s, b) 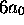 dans l'état 2s.
dans l'état 2s.
- Calculez <r> dans les états
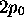 et 3s. Vérifiez que votre
résultat suit bien la formule générale suivante:
et 3s. Vérifiez que votre
résultat suit bien la formule générale suivante:
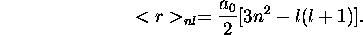
- Calculez
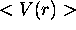 dans l'état 1s, où
dans l'état 1s, où 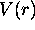 est le potentiel
de Coulomb de l'eq.3.2. Vérifiez que cette valeur moyenne de
est le potentiel
de Coulomb de l'eq.3.2. Vérifiez que cette valeur moyenne de
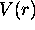 vaut
vaut 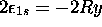 . (Utilisez l'
. (Utilisez l'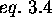 pour exprimer le potentiel
pour exprimer le potentiel 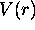 en coordonnées relatives).
en coordonnées relatives).
- Calculez
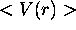 dans un état
dans un état 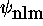 quelconque.
Vérifiez la relation générale suivante
quelconque.
Vérifiez la relation générale suivante
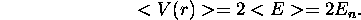
Cette relation implique que 2<T> + <V> = 0 dans tout état stationnaire de l'atome, T étant l'énergie cinétique de l'électron. Ce résultat s'appelle le théorème du viriel.