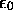 et
et 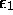 , de la molécule de NO sont exceptionnellement
rapprochés, la distance qui les sépare étant
, de la molécule de NO sont exceptionnellement
rapprochés, la distance qui les sépare étant  . La fréquence vibrationnelle de NO
est
. La fréquence vibrationnelle de NO
est  dans les deux états é
lectroniques concernés.
dans les deux états é
lectroniques concernés.
- Calculez le rapport
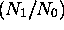 des populations de ces deux
niveaux à
des populations de ces deux
niveaux à  .
.
On constatera que le premier niveau excité est appréciablement peupl é à cette température. Il doit donc être inclu dans la fonction de répartition électronique avec l'état fondamental.
- Calculez la contribution électronique à la capacité
calorifique molaire de NO à
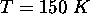 .
.
- La valeur de
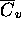 mesuré à
mesuré à 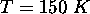 équivaut à
équivaut à 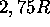 . Comparez cette valeur expérimentale à celle prédite par
la théorie en tenant compte de la contribution de tous les mouvements
dont est animée la molécule.
. Comparez cette valeur expérimentale à celle prédite par
la théorie en tenant compte de la contribution de tous les mouvements
dont est animée la molécule.
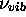 équivaut à un
quantum d'énergie
équivaut à un
quantum d'énergie 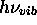 de
de 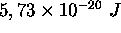 pour la mol
écule HCl et de
pour la mol
écule HCl et de  pour
pour 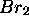 .
.
- Calculez le rapport
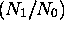 entre la population du premier
niveau d'énergie vibrationnelle excité (v=1) et celle du niveau
fondamental (v=0) pour ces deux espèces diatomiques, à
entre la population du premier
niveau d'énergie vibrationnelle excité (v=1) et celle du niveau
fondamental (v=0) pour ces deux espèces diatomiques, à  .
.
- Calculez la contribution vibrationnelle à la capacité
calorifique de
- une mole de HCl,
- une mole de
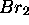
à
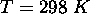 .
.
- une mole de HCl,
 est
triplement dégénéré. Le premier niveau électronique excit
é est doublement dégénéré et se situe à
est
triplement dégénéré. Le premier niveau électronique excit
é est doublement dégénéré et se situe à 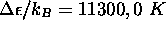 du fondamental. Les autres états é
lectroniques se situent à des niveaux encore plus élevés. On les
négligera dans ce qui suit.
du fondamental. Les autres états é
lectroniques se situent à des niveaux encore plus élevés. On les
négligera dans ce qui suit.
- Dans quelle gamme de température les mouvements électroniques
dans la molécule commenceront-ils à apporter une contribution non-n
égligeable à la capacité calorifique d'une mole de
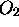 ?
?
- Calculez la capacité calorifique
 totale d'une mole de
totale d'une mole de 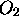 à
à 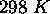 ,
, 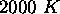 et
et 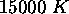 , sachant que la fréquence
vibrationnelle de
, sachant que la fréquence
vibrationnelle de 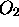 vaut
vaut 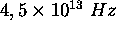 .
.
 sous le premier niveau électronique excité qui est
doublement dégénéré. Les autres niveaux électroniques
sont plus éloignés et peuvent être négligés. Calculez la
fonction de répartition électronique et la contribution é
lectronique à la capacité calorifique d'une mole de
sous le premier niveau électronique excité qui est
doublement dégénéré. Les autres niveaux électroniques
sont plus éloignés et peuvent être négligés. Calculez la
fonction de répartition électronique et la contribution é
lectronique à la capacité calorifique d'une mole de  à i)
à i)  , ii)
, ii)  et iii)
et iii) 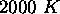 .
.
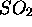 a trois modes normaux de vibration de fré
quences
a trois modes normaux de vibration de fré
quences  , i=1,2,3, avec
, i=1,2,3, avec

- Calculez la fonction de répartition vibrationnelle et la
contribution vibrationnelle à l'énergie moyenne et à la
capacité calorifique d'une mole de
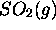 à
à 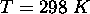 .
.
- Calculez la capacité calorifique totale d'une mole de
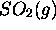 à
à 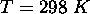 en tenant compte de tous les mouvements moléculaires et
en supposant une excitation électronique négligeable à cette
température.
en tenant compte de tous les mouvements moléculaires et
en supposant une excitation électronique négligeable à cette
température.
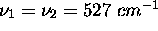 ,
, 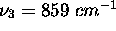 et
et 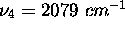 . Calculez la quantité de chaleur (
. Calculez la quantité de chaleur (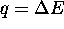 )
absorbée par une mole de
)
absorbée par une mole de 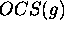 au cours d'un chauffage de
au cours d'un chauffage de  à
à  .
.