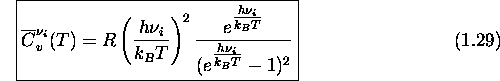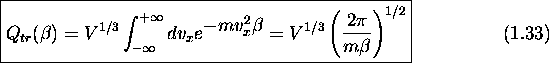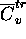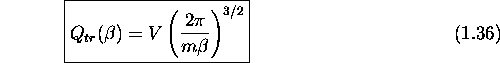Mouvements moléculaires particuliers

1. Mouvements électroniques: On a vu, à la section pr écédente qu'à cause de leur grand éloignement, les niveaux électroniques excités d'une molécule ne sont géné ralement pas occuppés dans des conditions de températures habituelles. Ce qui fait que, typiquement,
   • la fonction de répartition électronique a la forme

      

   • l'énergie moyenne se réduit à 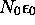, l' énergie de l'état fondamental

      

     Elle est donc indépendante de T,

   • et est nulle

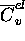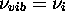2. Vibrations: Pour un mode vibrationnel de fréquence dont l'énergie est quantifiée selon eq.(1.3), on trouve que
   • la fonction de répartition prend exactement la forme

      

   • l'énergie moyenne est donnée par

      

   • et 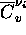est donnée par

      

   Notons deux limites intéressantes de et de :

   • à basse température,

     

     et

     

     Cette limite est en fait pratiquement atteinte pour o ù

     

     est appellée température vibrationnelle du ième mode.

   • à température élevée, ,

     

     et

     

     À une température où l'énergie thermique 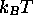dé passe largement les quanta d'énergie 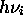des modes de vibrations moléculaires, chaque mode contribue donc RT à l'énergie moyenne, et R à la capacité calorifique molaire. On dit qu'on a équipartition de l'énergie: grosso-modo, ce principe dit que chaque composante de l'énergie de mouvement, qu'elle soit de nature cinétique ou potentielle contribue, à haute température, la même quantité, , à l'énergie moyenne, donc à la capacité calorifique, pourvu que cette composante est harmonique, c. à d. qu'elle est quadratique soit dans la vitesse 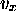, ou dans la position x.

3. Rotations: Avec les niveaux d'énergie rotationnelle donn és par eqs.(1.5-1.7), et tenant compte de leur dé générescence, eqs.(1.8-1.8), on trouve, dans une très bonne approximation, et pour
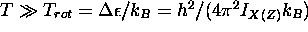
   • que la fonction de répartition rotationnelle est proportionnelle à T dans le cas d'une molécule linéaire et à 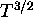dans les autres cas

      

   • l'énergie moyenne est donc donnée par

      

   • et 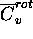est donnée par

      

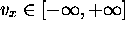4. Translations: L'énergie translationnelle étant pratiquement non-quantifiée et donnée, pour les translations dans une direction (x) déterminée, par eq.(1.10) avec , (dégénérescence = ), on a
   • fonction de répartition

      

   • énergie moyenne

      

   • 

      

   pour chaque direction de mouvement translationnel possible. Pour le mouvement de translation dans l'espace tridimensionnel, on a donc

   • fonction de répartition

      

   • énergie moyenne

      

   • 

      

   Notons que les mouvements de translation satisfont au principe d' équipartition de l'énergie pratiquement à toute tempé rature. Ce principe est aussi respecté dans le cas des rotations pour ce qui inclut généralement la température ambiante.