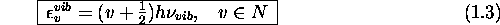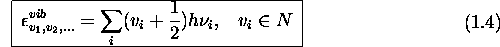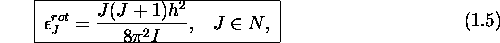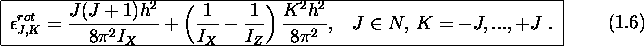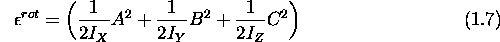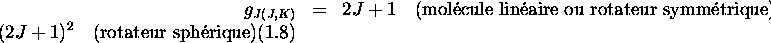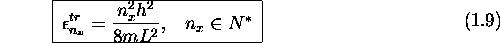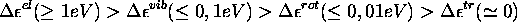- Il n'existe pas de formule de quantification générale
décrivant ces niveaux comme eq.(1.1) pour l'atome
d'hydrogène.
- Ces niveaux sont définis à des géométries nucléaires fixées. Ils dépendent des paramètres de géométrie nucléaire. Leurs variations avec la géométrie nucléaire engendrent des surfaces d'énergie potentielle (voir figure 1.2) qui régissent les mouvements nucléaires.
Notons qu'il existe des cas particuliers où les premiers niveaux électroniques sont plus rapprochés que décrits ci-haut. On verra des exemples de telles situations dans le cadre des exercices supplémentaires.

Figure: Surfaces d'énergie potentielle des états électroniques de 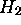
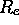 . Dans une bonne
approximation, qui asssimile les mouvements de vibrations avec ceux d'un
ressort élastique microscopique, l'énergie vibrationnelle est
quantifiée selon la loi simple suivante
. Dans une bonne
approximation, qui asssimile les mouvements de vibrations avec ceux d'un
ressort élastique microscopique, l'énergie vibrationnelle est
quantifiée selon la loi simple suivante
où 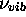 est la fréquence de vibration de la
molécule et
est la fréquence de vibration de la
molécule et
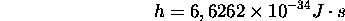
est la constante de Planck. Les caractéristiques des niveaux d'énergie vibrationnelle sont
- ils sont non-dégénérés
- leur séparation est typiquement

et les raies du spectre vibrationnelle se situent dans l'infra-rouge.
-
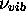 dépend de l'état électronique
dépend de l'état électronique
- la loi de quantification de eq.(1.3) est valide surtout à basse énergie. Dès que l'énergie augmente, et que l'on tend vers le seuil de dissociation, des corrections dues à des effets dits 'anharmonicités' sont nécessaires.
Une molécule polyatomique a plusieurs coordonnées
de vibrations, chacune correspondant à un mode de mouvement collectif
des noyaux, appellé mode normal de vibration. Une molécule
de N noyaux a 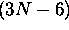 modes normaux de vibration si la molécule, au
repos, a une géométrie non linéaire. Dans le cas d'une
molécule linéaire, on compte
modes normaux de vibration si la molécule, au
repos, a une géométrie non linéaire. Dans le cas d'une
molécule linéaire, on compte 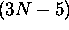 modes normaux de vibration.
Les figures 1.3 et 1.4 illustrent ceci pour
deux molécules, la molécule non linéaire
modes normaux de vibration.
Les figures 1.3 et 1.4 illustrent ceci pour
deux molécules, la molécule non linéaire 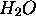 , et la
molécule linéaire
, et la
molécule linéaire 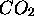 respectivement. Dans l'approximation
harmonique, l'énergie de chaque mode (de fréquence
respectivement. Dans l'approximation
harmonique, l'énergie de chaque mode (de fréquence 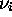 ) est
quantifiée selon la même loi que eq.(1.3), de sorte
que l'énergie vibrationnelle totale est donnée par
) est
quantifiée selon la même loi que eq.(1.3), de sorte
que l'énergie vibrationnelle totale est donnée par
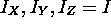 ). On distingue:
). On distingue:
- les rotateurs sphériques, avec
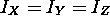 ,(Ex:
,(Ex: 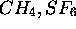 ),
),
- les molécules linéaires, avec
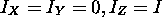 ,(Ex: molécules diatomiques,
,(Ex: molécules diatomiques, 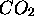 ,
, 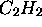 )
)
- les rotateurs symétriques, caractérisés par
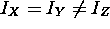 (
(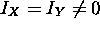 ), (Ex:
), (Ex: 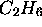 ,
, 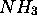 )
)
- les rotateurs asymétriques, avec
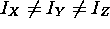 .
.
dans le cas des molécules linéaires et dans celui des rotateurs sphériques. Dans le cas d'un rotateur symétrique, l'énergie rotationnelle est quantifiée selon la loi
Le cas d'un rotateur asymétrique est trop complexe pour être traité exactement en mécanique quantique. On utilise l'expression classique de l'énergie rotationnelle écrite en fonction de 3 angles de rotation (angles d'Euler, 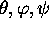 ) et de leur impulsion conjuguée (
) et de leur impulsion conjuguée (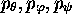 ):
):
où A, B, C sont des fonctions de 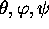 et de
et de 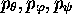 .
.
Les caractéristiques des niveaux d'énergie rotationnelle sont
- ils sont séparés par des distances typiques de l'ordre du
centième de l'électron-volt

ce qui donne des raies spectrales dans la région des micro-ondes.
- un niveau
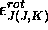 donné a une
dégénérescence
donné a une
dégénérescence
- les moments d'inertie
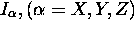 dépend de l'état électronique
où se trouve la molécule.
dépend de l'état électronique
où se trouve la molécule.
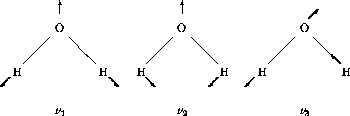
Figure 1.3: Les trois modes normaux de vibration de la molécule non linéaire
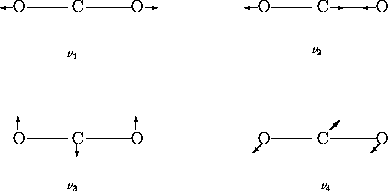
Figure 1.4: Les quatre modes normaux de vibration de la molécule non linéaire 
où m est la masse moléculaire et L est la longeur de la boite unidimensionnelle. Quand celle ci est de dimension macroscopique, les niveaux décrits par eq.(1.9) sont tellement rapprochés qu'on peut considérer l'énergie translationnelle non quantifiée. On écrirait plutôt