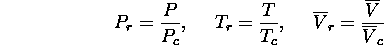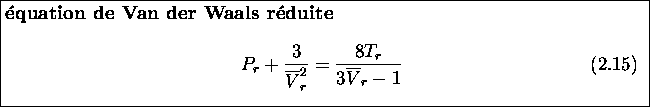Il est utile de comparer les courbes 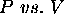 à T constante, encore appelées les isothermes, associées à l'équation d'état de Van der Waals avec celles d'un gaz parfait, et celles d'une substance réelle, figure 2.3. Dans le cas de l'équation d'état d'un gaz parfait, P décroit monotonement avec V, tandis que la variation de
à T constante, encore appelées les isothermes, associées à l'équation d'état de Van der Waals avec celles d'un gaz parfait, et celles d'une substance réelle, figure 2.3. Dans le cas de l'équation d'état d'un gaz parfait, P décroit monotonement avec V, tandis que la variation de 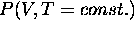 est non-monotone dans les deux autres cas pour une certaine gamme de température, inférieure à la température dite critique,
est non-monotone dans les deux autres cas pour une certaine gamme de température, inférieure à la température dite critique,  , où la courbe
, où la courbe 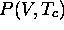 passe par un point d'inflexion. Dans le cas de l'équation de Van der Waals, ce point d'inflexion bifurque à
passe par un point d'inflexion. Dans le cas de l'équation de Van der Waals, ce point d'inflexion bifurque à 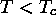 pour donner un maximum local et un minimum local. Les variables d'état au point critique
pour donner un maximum local et un minimum local. Les variables d'état au point critique  sont alors obtenues par les conditions
sont alors obtenues par les conditions

qui donnent,
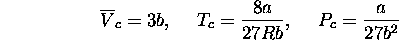
ou encore
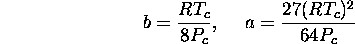
Le point critique marque le début de la zone d'existence de l'état liquide. À cet égard, il est intéressant de noter que dans le cas réel, le point d'inflexion (le point critique), au lieu de bifurquer en un maximum et un minimum local, se dégénère en une ligne de coexistence gaz-liquide. Dans le cas de l'équation de Van der Waals, la non-constance de P dans la région de coexistence de ces deux phases (l'existence des minimum et maximum) est un défaut du modèle.
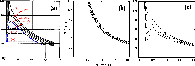
Figure: Isothermes (a) expérimentales, (b) de gaz parfait, (c) de Van der Waals, de  , tracées pour
, tracées pour 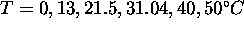 .
.
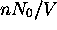 , donc à l'inverse du volume molaire
, donc à l'inverse du volume molaire 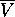 , au carré. Pour en tenir compte, on peut simplement remplacer P par
, au carré. Pour en tenir compte, on peut simplement remplacer P par 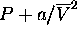 dans l'équation des gaz parfaits.
dans l'équation des gaz parfaits.
 disponible au libre parcours des
disponible au libre parcours des 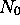 molécules de la mole de gaz. On doit donc remplacer
molécules de la mole de gaz. On doit donc remplacer 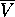 par
par  au second membre de l'équation des gaz parfaits.
au second membre de l'équation des gaz parfaits.
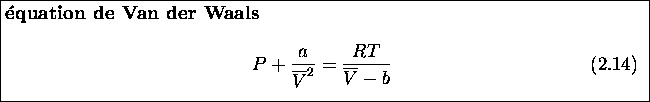
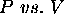 à T constante, encore appelées les isothermes, associées à l'équation d'état de Van der Waals avec celles d'un gaz parfait, et celles d'une substance réelle, figure
à T constante, encore appelées les isothermes, associées à l'équation d'état de Van der Waals avec celles d'un gaz parfait, et celles d'une substance réelle, figure 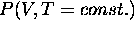 est non-monotone dans les deux autres cas pour une certaine gamme de température, inférieure à la température dite critique,
est non-monotone dans les deux autres cas pour une certaine gamme de température, inférieure à la température dite critique,  , où la courbe
, où la courbe 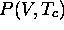 passe par un point d'inflexion. Dans le cas de l'équation de Van der Waals, ce point d'inflexion bifurque à
passe par un point d'inflexion. Dans le cas de l'équation de Van der Waals, ce point d'inflexion bifurque à 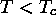 pour donner un maximum local et un minimum local. Les variables d'état au point critique
pour donner un maximum local et un minimum local. Les variables d'état au point critique  sont alors obtenues par les conditions
sont alors obtenues par les conditions

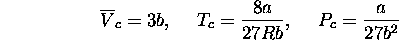
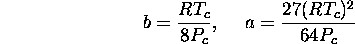

 , tracées pour
, tracées pour 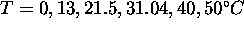 .
.