Considérons la réaction réversible suivante
où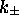 
sont des constantes de vitesse du premier
ordre. Cette réaction est en fait une séquence de deux réactions
élémentaires du premier ordre: la première, de constante de vitesse 
est appellée réaction ou étape directe, la
seconde, de constante de vitesse 
est appellée réaction ou
étape opposée. Les concentrations de 
et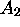 
obéissent
aux lois de vitesse suivantes
En utitilisant l'équation de conservation de masse
ces équations de vitesse couplées peuvent être
transformées en une équation unique gouvernant l'une des deux
concentrations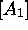 
, 
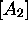
Définissons
alors, l'équation (6.5) se réduit à
ce qui représente une loi de vitesse effective du premier ordre. Elle s'intègre immédiatement en
Le degré d'avancement 
suit donc exactement une
cinétique du premier ordre de constante de vitesse effective 
,
ce qui donne
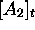est alors donnée par eq.(6.4).
Dans le cas particulier où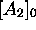 
est nulle, on a
Il est intéressant d'examiner le comportement de cette solution particulière dans les deux limites suivantes
,
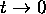À temps court, la dynamique du système est dominée par
l'étape directe, une réaction du premier ordre de constante de
vitesse 
.
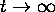, eqs.(6.10) et (6.11) se réduisent à
de sorte que
Il en est de même pour la vitesse de formation de 
. La
limite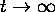 
correspond donc à l'état d'
équilibre du système et les concentrations de 
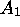et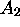 
dans cette limite, 
, 
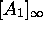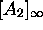, définissent
des concentrations à l'équilibre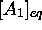 
, 
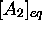. Remarquons que le degré d'avancement 
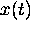défini
auparavant à l'équation (6.6) est mesuré par rapport
à l'état d'équilibre.
Des équations (6.14)-(6.16), on obtient une relation importante, la relation entre
