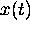Imaginons que l'on perturbe le système réactionnel
pour le mettre légèrement hors d'équilibre. Le retour du système
vers l'état d'équilibre est appellé relaxation. C'est la
cinétique de ce processus de relaxation qui nous intéresse ici. Comme
l'état initial du système est proche de l'état d'équilibre, le
degré d'avancement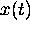 
défini par
par rapport à l'état d'équilibre, est à tout temps faible, c.à d.
Dans l'équation de vitesse (6.19),
ré-écrit en termes de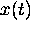 
,
on peut alors négliger les termes en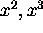 
, etc.,
et obtenir une loi de vitesse effective du premier ordre par rapport à x
: la cinétique de relaxation est toujours du premier ordre. Un
nombre d'exemples simples permettent de vérifier cette affirmation:
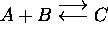L'équation de vitesse (6.24) s'écrit
plus explicitement sous la forme
À cause de la relation entre 
et les constantes de vitesse 
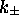, eq.(6.21), le dernier terme à la seconde ligne de
eq.(6.25) est nulle. L'avant-dernier terme est du second ordre en
x, et peut-être négligé. On obtient alors
L'inverse de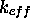 
définit un temps, appellé
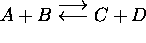L'équation de vitesse (6.24) s'écrit
Encore une fois, à cause de la relation entre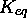 
et les constantes
de vitesse 
, eq.(6.21), le dernier terme est nulle.
L'avant-dernier terme est du second ordre en x, et peut-être néglig
é. On obtient alors
Ici, 
est donnée par
La généralisation des considérations précédentes donne
c.à d. que la constante de vitesse effective 
caractérisant la cinétique (du premier ordre) de relaxation est une
combinaison linéaire des constantes de vitesses individuelles 
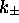avec
coefficients dépendant des concentrations d'équilibre des différentes
espèces. Il faut bien noter que cette généralisation n'est valable que si
les deux étapes directe et opposé sont, ou se comportent comme, des réactions
élémentaires.
