Soit la séquence de réactions du premier ordre suivante:
qui est décrite par les équations de vitesse suivantes:
La première de ces trois équations s'intègre immédiatement pour donner
Substituant ceci dans la seconde équation de vitesse, et intégrant, on
obtient, dans le cas où seul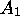 
était présent initialement, c. à
d. 
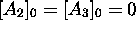
tandis que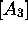 
s'obtient en utilisant la conservation de masse
ce qui donne
Les figures 6.1 et 6.2 montrent la variation
des concentrations 
, 
, 
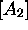en fonction du temps pour deux
cas extrêmes:
(figure 6.1): Dans ce cas, la
vitesse de formation de 
est bien plus faible que la vitesse de
consommation de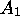 
à tout temps,
et la formation du produit final est cinétiquement contrôlée par
la seconde étape. Ceci se lit trivialement sur l'équation de vitesse
pour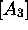 
, et aussi sur la forme intégrale de eq.(6.40
) qui, dans la limite 
tend vers
Dans ce cas on dit que la seconde étape, de constante de vitesse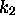 
, est l'étape déterminante pour la formation du produit 
.
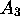. Dans ce cas, illustré à la figure 6.2, la concentration de l'espèce intermédiaire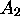 
demeure à tout temps très faible et ses variations sont pratiquement
invisibles. On peut alors écrire, à tout temps:
ou encore
L'approximation que l'on vient d'introduire constitue l'hypothè se de l'état stationnaire. Elle est souvent utilisée dans l'analyse des mécanismes de réactions complexes. Si l'on substitue eq.(6.44) dans eq.(6.36), on obtient
ce qui signifie que la cinétique de formation du produit 
est
contrôlée par la première étape. C'est cette étape qui
est l' étape déterminante dans ce cas. Par ailleurs, de eq.(
6.40), on vérifie que, dans la limite 
,
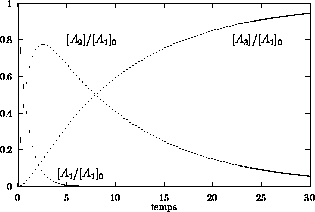
Figure 6.1: variation des concentrations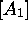 
, 
, 
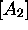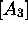en fonction du temps pour le cas 
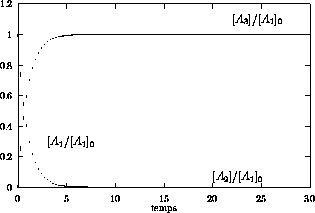
Figure 6.2: variation des concentration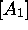s 
, 
, 
en fonction du temps pour le cas 
