L'énergie minimum requise pour ioniser un atome d'un certain solide par effet photoélectrique est égale à 3.44×10^-18J.

1. Calculer la longueur d'onde d'une radiation qui provoque l'éjection d'un électron de la surface de ce métal avec une vitesse de 1.08×10⁶ m.s^-1.
2. Porter en graphique la variation de l'énergie cinétique des électrons arrachés à la surface de ce métal en fonction de la fréquence de la radiation électromagnétique incidente.

a) 50.0 nm

Dans une étude de l'effet photoélectrique sur la surface d'un certain métal, on a obtenu les résultats suivants:

λ (nm)	405	436	480	520	578	650
Ecinétique (eV)	1.535	1.288	1.027	0.866	0.607	0.371

1. Les données d'une seule colonne du tableau suffisent pour calculer la fréquence seuil. Expliquez pourquoi on préfère cependant une méthode utilisant tous les points.
2. Calculez la fréquence seuil du césium;
3. Dans quel domaine de longueur d'onde peut-on arracher des électrons de la surface du métal?
4. Quelle est la valeur de la constante de Planck calculée à partir de ces résultats?
5. Données

a) 3.710×10¹⁴ Hz; b) λ ≤ 808 nm; c) h = 6.60×10^-34 J.s^-1. Solution

La couleur bleue des feux d'artifice est obtenue généralement par chauffage de CuCl à environ 1200°C. La longueur d'onde de la radiation émise est de 450 nm. Quelle est la valeur du quantum d'énergie émis par CuCl? Exprimez le résultat en J, puis en eV. 4.41×10^-19J ou 2.755 eV

Une lampe à vapeur de sodium d'une puissance de 100 W émet un rayonnement électromagnétique de longueur d'onde λ=550 nm. Combien de quanta d'énergie la lampe émet-elle par seconde? 2.77×10 ²⁰

Compléter le tableau suivant. Quelle est, de l'ultraviolet ou de l'infrarouge, la radiation la plus énergétique?

longueur d'onde de la radiation électromagnétique	énergie d'un quantum		énergie d'une mole de quanta
	(J)	(eV)	(kJ.mol-1)
600 nm
200 nm
150 pm
1 cm

Tableau complété - Radiation la plus énergétique: celle de plus petite longueur d'onde, donc l'UV.

La rétine de l'œil humain est capable de détecter toute source lumineuse émettant une énergie d'au moins 4×10^-7J. À combien de quanta de longueur d'onde 600 nm cela correspond-il? 1.21×10¹²

La quantité de chaleur requise pour faire fondre un gramme de glace en eau à 0°C est 333.5 J. Combien de molécules d'eau chaque quantum de longueur d'onde 660 nm fait-il fondre? 30 — Solution détaillée

On considère trois niveaux d'énergie permis d'une molécule E₁, E₂ et E₃, en ordre croissant. La transition de E₃ à E₂ s'accompagne de l'émission d'un photon de longueur d'onde 984 nm. La transition de E₂ à E₁ s'accompagne de l'émission d'un photon de longueur d'onde 495 nm. Quelle est la longueur d'onde du photon émis lors de la transition de E₃ à E₁? schéma de la transition — 329 nm

Expliquer pourquoi le fait que les atomes émettent un spectre de raies et non un spectre continu, indique que leur énergie est quantifiée. Solution détaillée

En postulant que l'énergie des atomes est quantifiée, Max Planck (Prix Nobel 1918) a pu expliquer la catastrophe dans l'ultraviolet dans le spectre d'émission du corps noir. Il a montré que l'intensité émise est maximum pour une longueur d'onde λ_max telle que:

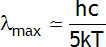
où k est la constante de Boltzmann et T la température (en K). Le filament de tungstène d'une ampoule électrique est un corps noir chauffé par le courant qui le parcoure. À quelle température doit-on chauffer le filament pour que le maximum du spectre électromagnétique émis se situe à 550 nm? 4959ºC

Dans le modèle de Bohr, quelle est l'énergie potentielle de l'électron de l'atome d'hydrogène lorsqu'il est placé à une distance égale à 0.529Å du proton? E_pot = -4.361×10^-18J

Quelles sont les raies de plus petite et de plus grande longueur d'onde dans les séries de Lyman, Balmer et Paschen pour l'atome d'hydrogène? Indiquer dans quel domaine du spectre électromagnétique ces ondes se situent. Lyman: 91.1(UV) et 121.5 nm (UV); Balmer: 364.5 (UV proche) et 656.5 nm (visible); Paschen: 820.1 (proche IR) et 1875 nm (IR)

On a trouvé dans l'espace interstellaire des atomes d'hydrogène excités avec un nombre quantique n égal à plusieurs centaines. Calculez la longueur d'onde émise lorsqu'un atome d'hydrogène subit une transition de n=236 à n=235. Dans quel domaine du spectre électromagnétique cette longueur d'onde se trouve-t-elle? 59.51 cm (ondes radio)

Le modèle de Bohr permet de prédire les spectres de raies des atomes ou des ions possédant un seul électron. C'est le cas en particulier de l'ion He⁺, dont certaines raies sont données dans le tableau ci-dessous.

ni	nf	longueur d'onde de la   radiation émise λ (nm)
2	1	30.380
3	1	25.633
3	2
4	2

1. Compléter le tableau.
2. Calculer l'énergie d'ionisation de l'ion He⁺. Exprimer le résultat en J et en eV.
3. Comparer les énergies d'ionisation de He⁺ et de l'atome d'hydrogène. Proposer une explication pour la différence observée.

(a) 164.0 et 121.5 nm; (b) 8.718×10-¹⁸J ou 54.42 eV; (c) indice: charge du noyau.