Solution

Qu'est-ce que la catastrophe dans l'U.V.?

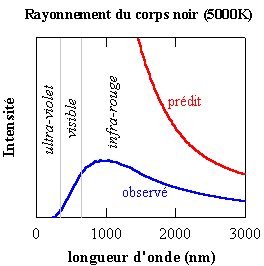
L'expression décrit une caractéristique du rayonnement électromagnétique émis par le corps noir. Le spectre (c'est-à-dire l'intensité émise en fonction de la longueur d'onde) présente un maximum dans le domaine de l'infra-rouge ou du visible. L'intensité émise diminue lorsque la longueur diminue, tendant vers zéro dans l'ultra-violet (UV). Or, les modèles de l'atome qui prévalaient avant les travaux de Max Planck et d'Einstein et l'hypothèse que l'énergie des atomes est quantifiée, prédisaient que l'intensité ne devrait pas passer par un maximum en fonction de la longueur d'onde, mais devait augmenter asymptotiquement lorsque la longueur d'onde diminue. On prédisait donc alors une grande intensité émise dans l'UV: tout devrait "briller" dans le noir!. C'est ce désaccord considérable entre la réalité expérimentale et les modèles de l'époque qu'on appelle catastrophe dans l'UV.

Est-ce normal d'obtenir une longueur d'onde négative losqu'on calcule la longueur d'onde émise dans le cas des spectres de raies?

C'est en effet ce que l'on obtient, si on oublie de considérer que ce que perd l'atome (changement d'énergie négatif) est exactement gagné par l'onde (changement d'énergie positif):
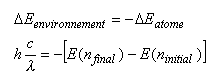
équation pour calcul du spectre de raies

équation pour calcul du spectre de raies

Quelle est la première raie de Lyman? Est-ce lors de la transition de n = +

à n=1 ou lors de la transition de n=2 à n=1?

Il peut s'agir de l'un ou l'autre puisqu'on peut placer les raies en ordre de fréquence croissante ou décroissante, ou encore par ordre de longueur d'onde. Il n'y a plus d'ambiguité cependant si on demande la première et la dernière raies de Lyman (comme dans l'exercice 2.7), puisqu'il faudra alors répondre en donnant les fréquences ou les longueurs d'onde correspondant aux deux transitions.

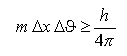Qu'est-ce que cela signifie lorsqu'on dit que le principe d'incertitude de Heisenberg donne les limites en dessous desquelles tout objet possède essentiellement des propriétés ondulatoires? Comment déduit-on, à partir de l'équation, si un objet est décrit plutôt en termes de particule ou d'onde? Est-ce que le signe plus grand ou égal y est pour quelque chose?

Il est important de réaliser que le principe d'incertitude découle des propriétés ondulatoires que possède tout objet (et qui sont exprimées par la relation de De Broglie). Puisque l'onde en question est, pour simplifier, une onde de probabilité, il est logique que ces propriétés ondulaloires de la matière se traduise par une certaine limite sur la certitude (c'est-à-dire une probabilité de 100%) d'une détermination de la position ou de la vitesse de l'objet. Lorsque l'application du principe d'incertitude conduit à des résultats aberrants, par exemple une incertitude égale ou supérieure à 200 nm sur la position d'un électron autour du noyau, alors que la taille de l'atome est de l'ordre du nm, on pourra dire que parler de cette particule en termes de vitesse et de position n'a plus beaucoup de sens. Ce sont alors les propriétés ondulatoires qui décrivent le comportement de la particule et non plus x et

, des paramètres de mécanique classique.

Lorsqu'on calcule la longueur d'onde d'une radiation qui permet d'exciter un électron, par exemple un électron d'un atome de zinc d'une orbitale 4s à une orbitale 4p, pourquoi obtient-on une valeur négative de

En effet, si on respecte la convention de signe, on semble obtenir en apparence

<0:

E_atome = E_finale - E_intiale est positif, car E_finale>E_initiale
C'est un résultat conforme à la convention de signe car le système (ici l'atome) gagne de l'énergie. L'onde électromagnétique qui provoque cette excitation perd donc l'énergie et

E_{environnement}=E_{fournie par l'onde}<0. Cependant, l'énergie transportée par l'onde possède une valeur absolue (donc positive) égale à hc/

. Cela conduit à une valeur positive de

.
On retrouve souvent ce genre de considérations losqu'on parle d'énergie. Par exemple, si on fait parcourir un courant électrique d'intensité I dans une résistance électrique R pendant un temps t, on observe la production d'une énergie sous forme de chaleur égale en valeur absolue à RI²t. Cette énergie sera comptée positivement si la résistance appartient au système et négativement si la résistance appartient à l'emvironnement (le système étant par exemple l'objet que l'on chauffe). Dans tous les cas cependant, la résistance R est positive.

Si on compare les configurations électroniques de H₂ et H₂⁺, on remarque que l'électron de H₂⁺ est dans la même orbitale moléculaire liante

_1s que chacun des deux électrons de H₂. Pourquoi, si tous ces électrons ont sensiblement la même énergie, l'énergie de liaison est-elle plus grande et la liaison plus courte pour H₂?

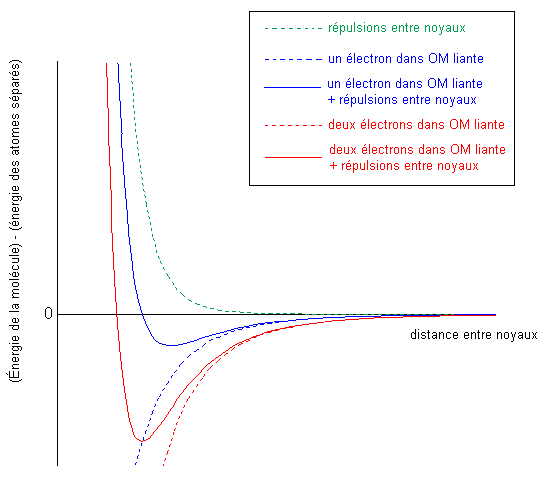La longueur et l'énergie de liaison sont déterminées par la position du minimum d'énergie de la molécule. La position du minimum dépend elle-même de chacune des contributions à l'énergie totale de la molécule. Lorsque l'orbitale moléculaire liante contient deux électrons, le minimum est plus profond (énergie de liaison plus grande) et à une distance plus petite entre les deux noyaux (liaison plus courte).

Pour ceux qui doutent des courbes ci-contre, ou qui veulent simplement jouer avec ces additions de différentes contributions, vous pouvez télécharger le fichier Excel© et varier les paramètres.

À quoi servent les orbitales hybrides? Pourquoi n'a-t-on pas toujours des liaisons entre orbitales atomiques pures? Dans quelle situation utiliser les orbitales hybrides?

Un examen détaillé du diagramme des énergies des OA, OA hybrides et OM dans le cas des hybrides sp dans l'acétylène (sur la page hybridation) peut fournir des éléments de réponse. Il est vrai que l'hybridation elle-même n'est pas favorable du point de vue de l'énergie, puisque l'énergie des sp se situe entre s et p et que, par conséquent, les deux électrons en sp ont une plus grande énergie qu'en 2s:

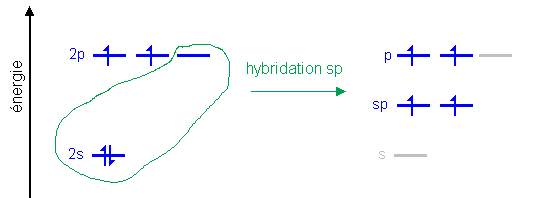
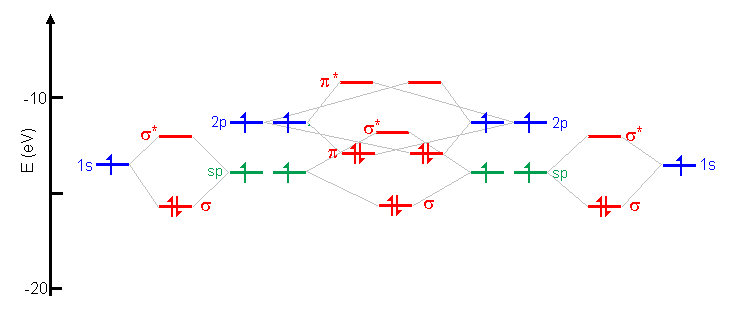
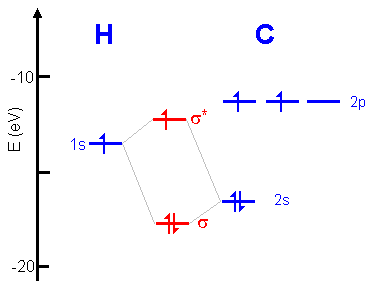
Cependant chacun de ces électrons initialement en sp occupe dans la molécule, après LCAO, une OM de type sigma dans laquelle son énergie est inférieure à celle qu'elle aurait été si les liaisons avaient été faites avec des OA non hybrides. Ainsi, dans C₂H₂ par exemple, tous les électrons de valence des deux H et des deux C se trouvent, grâce à l'hybridation, dans des orbitales moléculaires liantes:

On note que cela aurait été différent si la liaison C-H, par exemple, avait été construite à partir de C 2s (contenant deux électrons) et H 1s (avec un électron). On aurait alors dû placer ces trois électrons ainsi: 2 dans l'OM liante et 1 dans l'OM antiliante:

En résumé, l'hybridation est avantageuse sur le plan de l'énergie finale de la molécule. Cette énergie est inférieure si les OM sont construites à partir d'OA hybrides. Quant à savoir quand on peut prédire qu'il y aura hybridation ou non, c'est plus difficile et bien souvent, on sera guidé par la géométrie de la molécule, déterminée par ailleurs expérimentalement.