Énoncé
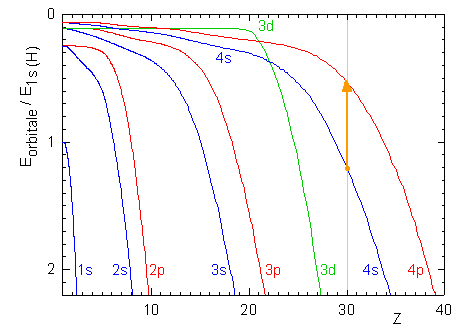
Déterminer, à l'aide de la figure donnant l'énergie des orbitales des atomes neutres en fonction de la charge du noyau:
- la longueur d’onde de la radiation électromagnétique capable d’exciter un électron d'un atome de zinc (Zn) d'une orbitale 4s à une orbitale 4p;
- l'énergie d’ionisation du sodium Na. Exprimer le résultat en électron-volts, en joules et en kilojoules par mole.
Solution
- Le tableau périodique nous fournit le numéro atomique du zinc, Z=30. L'énergie des orbitales du zinc sont donc données par l'intersection des courbes de la figure suivantes avec la ligne verticale à Z=30:
On lit ainsi E4p= 0.54 unités de l'échelle des énergies, soient 0.54×(-13.59)eV.
De la même manière, E4s=1.20×(-13.59)eV
La transition électronique d'une orbitale 4s à une orbitale 4p est représentée par la flèche orange. Elle s'accompagne d'un changement d'énergie de l'atome:
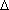 E = E4p-E4s = (0.54-1.20)×(-13.59) = 8.97 eV ou 1.44×10-18 J.
E = E4p-E4s = (0.54-1.20)×(-13.59) = 8.97 eV ou 1.44×10-18 J.
La longueur d'une onde électromagnétique capable de promouvoir cette transition est donnée par:
hc/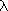 =
= 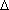 E
ce qui conduit à
E
ce qui conduit à 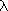 = 138 nm
= 138 nm
Note: pour clarifier la question du signe des énergies, voir la question pertinente de la foire aux questions.
-
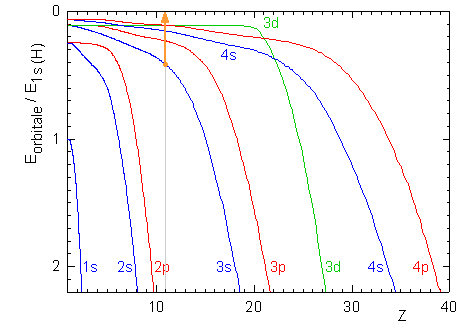
Le tableau périodique nous fournit le numéro atomique du sodium, Z=11, et sa configuration électronique: 1s2 2s2 2p6 3s.
La première ionisation consiste à porter l'électron qui, dans le sodium à l'état fondamental, possède l'énergie la plus élevée, jusqu'à une distance infinie du noyau, ou encore une énergie nulle. Cela correspond à la transition représentée par une flèche orange dans:
L'énergie nécessaire est I1 = 0 - E3s = -(0.41×-13.59) = 5.56 eV ou 8.91×10-19 J ou encore 554 kJ.mol-1