Structure moléculaire

Exercices du Chapitre 6: Propriétés électriques des molécules


6.1 Un condensateur plan possède la géométrie suivante: distance d = 0.2 cm; surface A = 100 cm2. On applique une différence de potentiel DELTAV=200 V que l'on maintient constante pendant toute l'expérience. Calculer la capacité du condensateur et la charge de chaque face lorsque
  1. le condensateur est placé sous vide;
  2. le condensateur est rempli avec un milieu de constante diélectrique epsilon/epsilono = 2.0
Réponses: (a) Co=4.427×10 -11 F; Qo = 8.854×10 -9 C; (b) C = 2Co ; Q = 2Qo .

6.2 Calculer le moment dipolaire induit dans une molécule d'eau par un champ électrique de 1.0 kV.cm-1.
Réponse: 4.8 µD.

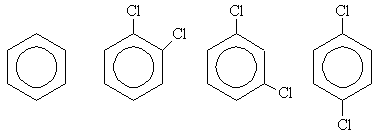
6.3 Représenter, schématiquement et sur la même figure, la polarisation molaire des quatre composés suivants en fonction de l'inverse de la température. Justifier le tracé.
dichlorobenzènes

6.4 La constante diélectrique du dioxyde de soufre SO2 gazeux, mesurée sous une pression constante égale à 1 atm, est 1.00993 à 0°C et 1.00569 à 100°C.
  1. En supposant que SO2 est un gaz parfait, calculer son moment dipolaire.
  2. La molécule de SO2 possède-t-elle la même géométrie que CO2 ? Pourquoi ?
Réponses: (a) µ = 1.634 D; (b) non, car son moment dipolaire n'est pas nul, ce qui indique que la l'angle O-S-O n'est pas 180°.

6.5
On a mesuré la constante diélectrique epsilon/epsilono de CH3Cl (g) à volume constant en fonction de la température:
  T (K)      epsilon/epsilono   
291.2  1.009789 
342.8 1.008448
366.5 1.007847
387.4 1.007387
414.6 1.006912
La pression à 291.2 K était égale à 713.9 mm de mercure. En supposant que CH3Cl se comporte comme un gaz parfait, calculer son moment dipolaire permanent et sa polarisabilité. Que peut-on déduire des résultats concernant la validité de la méthode?

6.6
On a mesuré la densité et la constante diélectrique du chloroforme CHCl3 liquide et solide en fonction de la température:
  T (°C)     d (g.cm-3)      epsilon/epsilono   
-80 1.65 3.1
-70 1.64 3.1
-60 1.64 7.0
-40 1.61 6.5
-20 1.57 6.0
0 1.53 5.5
20 1.50 5.0
Calculer la polarisation molaire PM à chaque température. Tracer PM en fonction de l'inverse de la température, Comment peut-on, à partir de ce graphique, calculer la polarisabilité alpha et le moment dipolaire µ du chloroforme? Expliquer ce que l'on observe au point de fusion (-64°C).

6.7
Calculer la polarisabilité de CH4 (g), CCl4(g) et CCl4(l) à partir des résultats expérimentaux donnés ci-dessous. Expliquer les différences observées.
 substance    T (K)     P (mm Hg)     d (g.cm-3)      epsilon/epsilono   
CH4 (g) 291.7 713.9    1.00084 
CCl4(g) 360.8 687   1.00273
CCl4(l) 298.2   1.585 2.228
alpha = 3.146×10 -40, 13.13×10 -40 et 12.43×10 -40 unités SI pour CH4 (g), CCl4(g) et CCl4(l), respectivement.
6.8
On a mesuré la constante diélectrique de la vapeur de BrF5 en fonction de la température, sous pression atmosphérique constante (P = 1 atm):
  T (K)      epsilon/epsilono   
345.6  1.006320 
362.6 1.005824
374.9 1.005525
388.9 1.005180
402.4 1.004910
417.2 1.004603
430.8 1.004378
En supposant que BrF5 obéisse à l'équation d'état des gaz parfaits,
  1. Calculer la polarisation molaire PM à chaque température;
  2. calculer la polarisabilité alpha et le moment dipolaire µ.
Réponses: alpha = 8.14×10 -40 unités SI; µ = 1.53 D
fichier zip regroupant les tableaux de données, en format Excel pour télécharger les données des problèmes (fichiers Excel, regroupés dans un fichier zip)
version PDF de la première partie de ce fichier pour télécharger cette page en format PDF, en vue de l'imprimer.
Page précédente