L'hamiltonien décrivant les vibrations moléculaires dans l'approximation harmonique est donc
L'hamiltonien de (2.38) est clairement de forme
séparable: c'est une somme d'hamiltoniens unidimensionnels, chacun
ne dépendant que d'un seul mode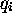 
comme variable, et décrivant ce
mode comme étant un ressort, ou oscillateur harmonique de masse
unitaire 
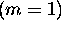et de fréquence 
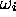. Par conséquent, une séparation
des variables 
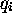est possible, réduisant l'équation de Schrödinger
indépendante du temps en 3N-6 (ou 3N-5) équations du même type que
celle d'un oscillateur harmonique unidimensionnel. Il suffit donc
de résoudre l'équation de Schrödinger unidimensionnelle
